Bonjour, je suis en 1erS. J'ai un dm sur les fonctions dérivées mais le problème est que je suis bloqué aux deux dernières questions. Voici le sujet :
On considère la fonction f définie sur R par :
f(x) = x^2-5x+4
1) soit "a" un réel, montrer que le taux d'accroissement de f entre a et a+h est égal à :
2a-5+h.
Pour cette question pas de problème.
2) En déduire que la fonction f est dérivable en a et déterminer f'(a).
Comme f est dérivable sur R alors f'(a) est aussi dérivable sur R et f'(a)= 2a-5
3) Montrer que l'équation réduite de la tangente à la courbe représentative de f au point A(a:f(a)) est donnée par : y = (2a-5)x-a^2+4
y = f'(a) (x-a) + f(a)
y = (2a-5)(x-a) + a^2-5a+4
y = 2ax - 2a^2 -5x +5a+a^2 -5a +4
y = 2ax -5x -a^2 +4
y = (2a-5)x -a^2+4
4) Existe-t'il un point de Cf pour lequel la tangente est horizonrale ?
Admettons que le point existe, on résou alors f'(x)=0
2x-5=0
2x=5
X=5/2
5) Existe-t'il un point de Cf pour lequel la tangente passe par l'origine du repère ?
Pour cette question je n'ai absolument aucune idée
6) Existe-t'il un point de Cf pour lequel la tangente est parallèle à la droite d'équation : y = x?
Je ne suis vraiment pas sûr mais je pense qu'il faut résoudre 2x-5=1 donc x = 3
Voilà merci de votre aide
Fonction dérivée 1erS
7 messages
- Page 1 sur 1
Re: Fonction dérivée 1erS
Bonjour,
4) Tes calculs sont bons mais pas explicités (quelle est ta démarche ?). De plus, tu n'as pas répondu à la question. Existe-t-il un point et si oui lequel ?
5) Tu dois d'abord chercher pour quelle(s) valeur(s) de a la droite Cf passe par l'origine
6) Même remarque que pour la question 4)
4) Tes calculs sont bons mais pas explicités (quelle est ta démarche ?). De plus, tu n'as pas répondu à la question. Existe-t-il un point et si oui lequel ?
5) Tu dois d'abord chercher pour quelle(s) valeur(s) de a la droite Cf passe par l'origine
6) Même remarque que pour la question 4)
Re: Fonction dérivée 1erS
Bonsoir,
Question 1.
D'accord...
Question 2.
1.) n'est pas une fonction mais un réel, donc "
n'est pas une fonction mais un réel, donc ") est dérivable" n'a pas de sens.
est dérivable" n'a pas de sens.
2. Quand tu écris) , tu supposes qu'il existe, donc tu sautes la première partie de la question.
, tu supposes qu'il existe, donc tu sautes la première partie de la question.
3. Reviens à la définition de la dérivée (limite de ...).
4. La valeur de) est correcte.
est correcte.
Question 3.
À part l'oubli de parenthèses à la deuxième ligne ((x-a)) et non
et non ) ), c'est bon...
), c'est bon...
Question 4.
1. Si tu admets qu'un tel point existe, il n'y a plus rien à montrer Or tu montres un résultat après...
Or tu montres un résultat après...
2. C'est plus un problème d'esthétique, mais puisque tu travaillais avec a, pourquoi changer et passer à x ?
3. Raisonne plutôt en écrivant des équivalences, comme ça tu sais que est bien l'unique point où la tangente est horizontale.
est bien l'unique point où la tangente est horizontale.
Question 5.
Tu connais l'équation de la tangente en :
: x-a^2+4) . Il faut qu'elle passe par l'origine du repère, donc par le point
. Il faut qu'elle passe par l'origine du repère, donc par le point ) ...
...
Question 6.
1. Deux droites parallèles ont même pente.
2. est une variable. Il faut que tu trouves les
est une variable. Il faut que tu trouves les  pour lesquels la tangente est parallèle à la droite d'équation
pour lesquels la tangente est parallèle à la droite d'équation 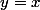 .
.
Question 1.
D'accord...
Question 2.
1.
2. Quand tu écris
3. Reviens à la définition de la dérivée (limite de ...).
4. La valeur de
Question 3.
À part l'oubli de parenthèses à la deuxième ligne (
Question 4.
1. Si tu admets qu'un tel point existe, il n'y a plus rien à montrer
2. C'est plus un problème d'esthétique, mais puisque tu travaillais avec a, pourquoi changer et passer à x ?
3. Raisonne plutôt en écrivant des équivalences, comme ça tu sais que
Question 5.
Tu connais l'équation de la tangente en
Question 6.
1. Deux droites parallèles ont même pente.
2.
Re: Fonction dérivée 1erS
Bonjour chombier et samoufar, merci pour votre aide.
QUESTION 2
D'après mon cours, il faudrait dire : le taux d'accroissement-f(a)}{h}) tend vers 2a-5 lorsque h tend vers 0. La fonction f est donc dérivable en a et f'(a) = 2a-5.
tend vers 2a-5 lorsque h tend vers 0. La fonction f est donc dérivable en a et f'(a) = 2a-5.
Est-ce juste ou non ?
QUESTION 4
Il serait donc correct de dire : Pour trouver si un tel point existe, il faut résoudre l'équation f'(a)=0.
On trouve .
.
Donc la tangente est horizontale au point d'abscisse 5/2
QUESTION 5
J'ai l'idée mais je n'arrive pas à formuler par une phrase :
On sait que la tangente d'équationx -a^2 + 4) doit passer par l'origine du repère donc par les coordonnées (0;0). On résout alors:
doit passer par l'origine du repère donc par les coordonnées (0;0). On résout alors:
0 - a^2 +4)



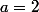
La tangente au point d'abscisse 2 de Cf passe donc par l'origine du repère.
QUESTION 6
Je ne comprends toujours pas. Pour que deux droites soient parallèles il faut quelles aient le même coefficient directeur. Dois-je donc résoudre l'équationx - a^2 + 4 = 1) ?
?
Merci encore.
QUESTION 2
D'après mon cours, il faudrait dire : le taux d'accroissement
Est-ce juste ou non ?
QUESTION 4
Il serait donc correct de dire : Pour trouver si un tel point existe, il faut résoudre l'équation f'(a)=0.
On trouve
Donc la tangente est horizontale au point d'abscisse 5/2
QUESTION 5
J'ai l'idée mais je n'arrive pas à formuler par une phrase :
On sait que la tangente d'équation
La tangente au point d'abscisse 2 de Cf passe donc par l'origine du repère.
QUESTION 6
Je ne comprends toujours pas. Pour que deux droites soient parallèles il faut quelles aient le même coefficient directeur. Dois-je donc résoudre l'équation
Merci encore.
Re: Fonction dérivée 1erS
Bonjour,
Question 2.
Ok !
Question 4.
Ok !
Question 5.
Bah si, tu arrives à formuler une phrase
Seul petit bémol, l'équation admet combien de solutions ?
admet combien de solutions ?
Question 6.
Encore une fois, est une variable. Quelle est le coefficient directeur de la droite donnée par la fonction
est une variable. Quelle est le coefficient directeur de la droite donnée par la fonction x-a^2+4) (fonction DE LA VARIABLE
(fonction DE LA VARIABLE  ) ?
) ?
Question 2.
Ok !
Question 4.
Ok !
Question 5.
Bah si, tu arrives à formuler une phrase
Seul petit bémol, l'équation
Question 6.
Encore une fois,
Re: Fonction dérivée 1erS
Bonjour
QUESTION 6
On sait que le coefficient directeur de la tangente est 2a-5 et celui de la droite d'équation y=x est 1. On résout alors :
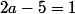
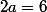
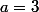
Il existe une tangente parallèle à la droite d'équation :y=x au point d'abscisse 3 de Cf.
Est-ce juste?
QUESTION 6
On sait que le coefficient directeur de la tangente est 2a-5 et celui de la droite d'équation y=x est 1. On résout alors :
Il existe une tangente parallèle à la droite d'équation :y=x au point d'abscisse 3 de Cf.
Est-ce juste?
Re: Fonction dérivée 1erS
Kisoov a écrit:QUESTION 6
On sait que le coefficient directeur de la tangente est 2a-5 et celui de la droite d'équation y=x est 1. On résout alors :
Il existe une tangente parallèle à la droite d'équation :y=x au point d'abscisse 3 de Cf.
Est-ce juste?
Bonjour,
QUESTION 5
a² - 2² = (a - 2)(a + 2) = 0
QUESTION 6
Je trouve aussi que l'on a une telle tangente à l'abscisse 3 :

Bonne journée.
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 57 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
