Factorielle

[t.itou29]

Bonsoir,
Je dois montrer que
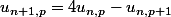
Il est demandé de montrer d'abord que (1)ce qui a été assez fastidieux ! Par récurrence j'ai supposé vrai la propriété à rang n alors au rang n+1 j'ai utilisé l'égalité (1) et l'hypothèse de récurrence sur mais pour le deuxième est-ce que possible avec p+1? je pense que comme l'hypothèse porte sur un p fixé elle est donc vraie aussi pour p+1 mais je sais pas si c'est correct.

[soradia1]

Slt est-ce-que tu peux préciser s'il y a d'autres hypothèses?! genre si n est plus grand ou plus petit que p, ou si p est premier ou pas.

[beagle]

"Il est demandé de montrer d'abord que..."
dommage car cea semble passer en direct,
d'abord p ne sert absolument à rien, on simplie par n! et par p!

reste à prouver que (n+2)(n+3)x...x(n+n) est divisible par n!
ce qui semble frisouille par récurrence

[hammana]

"Il est demandé de montrer d'abord que..."
dommage car cea semble passer en direct,
d'abord p ne sert absolument à rien, on simplie par n! et par p!

reste à prouver que (n+2)(n+3)x...x(n+n) est divisible par n!
ce qui semble frisouille par récurrence

Bonjour,

Je n'ai pas trouvé dans mon dictionnaire d'argot ce que veut dire frisouille?

Il est vrai que p ne sert à rien, d'ailleurs la relation

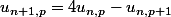
me parait fausse.
Je ne suis pas arrivé à démontrer que (n+2)(n+3)x...x(n+n)/n! est entier par la méthode de récurrence, par contre je peux montrer que tout facteur premier du dénominateur se retrouve au moins autant de fois au numérateur. Le problème est intéressant et mérite qu'on s'y attaque pour trouver une solution élégante

[beagle]

Bonjour,

Je n'ai pas trouvé dans mon dictionnaire d'argot ce que veut dire frisouille?

Il est vrai que p ne sert à rien, d'ailleurs la relation

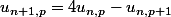
me parait fausse.
Je ne suis pas arrivé à démontrer que (n+2)(n+3)x...x(n+n)/n! est entier par la méthode de récurrence, par contre je peux montrer que tout facteur premier du dénominateur se retrouve au moins autant de fois au numérateur. Le problème est intéressant et mérite qu'on s'y attaque pour trouver une solution élégante

ah oui, frisouille, c'est en se frisant les moustaches,
bon ben non, cétait frisouille à 00h15mn heure à laquelle je devrais plutot dormir, car mes calculs hum hum...

[t.itou29]

Merci de vos réponses. Voici le lien pour l'énoncé exact de l'exercice
https://docs.google.com/file/d/0B2uj8lrnLJwSdEthNnZJN3hxOFk/edit?usp=sharing
Et pour la question intermédiaire si je me suis pas trompé la relation est vraie :
https://docs.google.com/file/d/0B2uj8lrnLJwSRGtYRzd6V19RYU0/edit?usp=sharing (désolé pour mon écriture!)
Dire que appartient a N par hypothèse de récurrence est vrai ou pas ?
Je vais essayer de réfléchir à trouver une solution sans question intermédiaire.
EDit: désolé je viens me rendre compte que j'ai fait une erreur dans l'énonce au déominateur c'est (n+p) et non (n+1) j'ai posté hier avant faire mes devoirs(les vraies pas des maths pour le plaisir!) et j'ai pas regardé depuis !

[chan79]

C'est plus facile, maintenant !

[t.itou29]

J'ai dû vous faire chercher pour rien. Du coup si je suppose entier pour un n quelconque alors est bien entier aussi comme l'hypothèse porte sur n et p est fixé?

[chan79]

J'ai dû vous faire chercher pour rien. Du coup si je suppose entier pour un n quelconque alors est bien entier aussi comme l'hypothèse porte sur n et p est fixé?

attention quand même à l'initialisation

[t.itou29]

attention quand même à l'initialisation

Je l'ai pas précisé mais pour n=0 on a , ce que j'ai dit dans le message précédent avec est bon ?

[chan79]

OK, ça marche

[t.itou29]

OK, ça marche

OK merci finalement c'était la première question qui prenait le plus temps en jouant avec les factorielles.