Raisonement par récurrence et Factorielle n
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 06 Sep 2010, 18:27
par girdav » 06 Sep 2010, 18:27
Bonjour,
quel est le rang initial?
En supposant la propriété vraie pour le rang

on doit montrer que
! \geq 3^{n+1})
. Pour cela, on peut écrire que
! =(n+1)n!\geq (n+1)3^n)
.
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 06 Sep 2010, 19:37
par girdav » 06 Sep 2010, 19:37
Quel est donc le

que tu as trouvé?
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 07 Sep 2010, 10:27
par girdav » 07 Sep 2010, 10:27
Pour
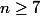
on a
! =(n+1)n! \geq 8.3^n\geq \cdots)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 25 invités