bonjour , j'ai un exo de mathematique a rendre prochainement sur les primitives ( je suis en T°S) mais ce n'est vrmt pas un niveau de terminal S voici l'enoncé jai reussi les premieres questions mais la fin je n'y arrive pas du tout si vous pouviez m"eclairer un petit peu . merci beaucoup:
On considere la fonction f definie sur R par f(x)=1/1+x^2 . F designe la primitive de f qui verifie F(0)=0 .
1. demontrer que F est une fonction impaire ( ca j'ai reussi )
2.on pose pour tout x appartenant a] -pi/2 ; pi / 2 [ h(x)= F(tan(x))
a) justiferque h est derivable sur l'intervalle ] -pi/2 ; pi / 2 [ et calculer sa dérivée ( j'ai reussi jai trouvé h'(x)=1 )
b) en conclure que l'on a F(tan(x)) = x ( jai reussi jai fait la primitive de h(x) )
c) en deduire la valeur exacte de F(1/2) et de F(1) ( jai trouvé F(1/2)= tan -1 de 1/2 et F(1) = pi/4 est ce cela ?
3. on pose G(x) = F(x) + F(1/x)
a) calculer sa dérivé ( je trouve aussi 1)
b) en deduire que F(x) = pi/2 - F(1/x) ( alors la jai pas du tout trouvé )
c) que vaut F(2) ? ( je pense que cest tan -1 de 2 )
d) determiner la limite de F(x) lorque x tend vers +00
e) en utilisant le fait que F est impaire determiner la limite de F lorque x tend vers -00 ( elle sera contraire a celle de +00 )
qu'en deduit t'on pour la courbe Cf ?
voila j'ai trouver quelque truc mais pas tout . merci bcp pour votre aide .
Exo tres tres tres compliqué !
7 messages
- Page 1 sur 1
jy_ha12 a écrit:3. on pose G(x) = F(x) + F(1/x)
a) calculer sa dérivé ( je trouve aussi 1)
Bj,
tout semble exact et dans l'esprit du problème sauf ça.
G est donc constante par intervalles.
mais le domaine de définition de G est constitué de 2 intervalles
et donne lieu à deux formules distinctes selon x>0 ou x<0.
On calcule la constante d'intégration en x=1 (et en x=-1)
en
explications "techniques":
La fonction F est effectivement la fonction
en effet , si gof(x)=x
donc
on a utilisé:
et une fonction à dérivée continue est une primitive de sa fonction dérivée.
Cette fonction
valeur de la tangente.
Comme certaines fonctions (elliptiques pour ne pas les nommer)
sont données et étudiées sous forme intégrale,
l'exercice que tu viens de traiter est considéré comme ...particulièrement intéressant
en marge de l'énoncé
signalons la très belle (et très obscure) formule
 + F(\frac{1}{2\sqrt{2}}))
De plus, comme l'intégrande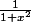 est la somme
est la somme
d'une série géométrique de raison (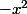 )
)
on peut écrire l'intégrande comme une limite de somme géométrique,
permuter limite et intégrale par continuité, et exprimer
 en fonction de
en fonction de 
De plus, comme l'intégrande
d'une série géométrique de raison (
on peut écrire l'intégrande comme une limite de somme géométrique,
permuter limite et intégrale par continuité, et exprimer
mathelot a écrit:signalons la très belle (et très obscure) formule
De plus, comme l'intégrandeest la somme
d'une série géométrique de raison ()
on peut écrire l'intégrande comme une limite de somme géométrique,
permuter limite et intégrale par continuité, et exprimeren fonction de
re,
on trouve par exemple
Salut, j'ai juste une petite question, pour la première question comme as-tu procéder ? As-tu utiliser la propriété : Une primitive d'une fonction paire pas forcément impaire, sauf si elle est définie sur un intervalle et si la primitive considérée est celle qui s'annule en 0
Ou alors y a un moyen très simple d'y arriver que je n'ai pas vu ?
Ou alors y a un moyen très simple d'y arriver que je n'ai pas vu ?
benekire2 a écrit:Salut, j'ai juste une petite question, pour la première question comme as-tu procéder ? As-tu utiliser la propriété : Une primitive d'une fonction paire pas forcément impaire, sauf si elle est définie sur un intervalle et si la primitive considérée est celle qui s'annule en 0
bah oui, c'est ça.
nous dérivons x--> P(x)=F(x)+F(-x) pour trouver une dérivée P' nulle.
La fonction est donc constante sur
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 68 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
