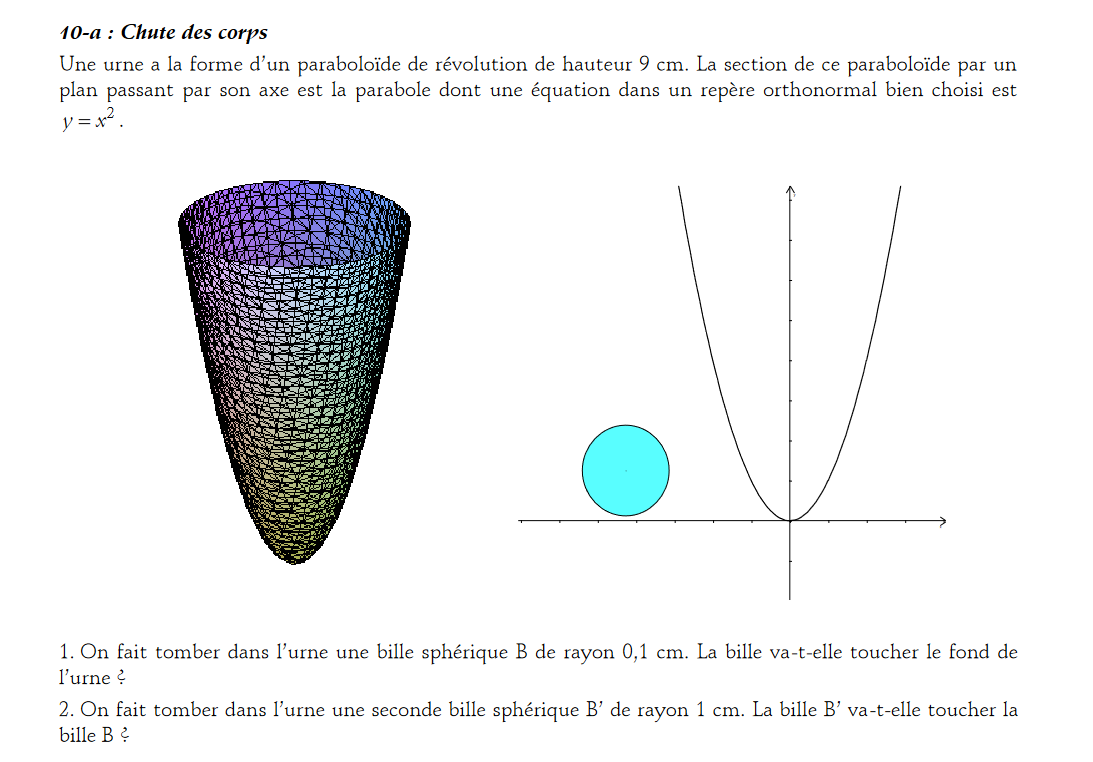
Les explications que je n'avais pas pu poster...
D'abord un résultat général
Soit T le point de tangence du cercle et de la parabole de coordonnées (t,t²) avec t>0.
L'équation de la normale en ce point est
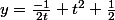
Le centre I du cercle tangent en T à la parabole, situé sur l'axe des ordonnées, est donc
)
Pour le premier cercle, soit T=A(t;t²) le point de tangence, le centre du cercle I a pour coordonnées (0;t²+0,5), le rayon du cercle est r=IA tel que r²=IA²=t²+0,25
donc t²=r²-0,25
Le point I a pour coordonnées (0;r²+0,25)
Le point C, plus haut point du premier cercle sur l'axe des ordonnées, a donc pour coordonnées (0;r²+r+0,25)
ou encore (0;(r+1/2)²) par la suite je noterai (0;c) ces coordonnées
Passons au deuxième cercle
On change de point de tangence, notons le B, mais le raisonnement est le même.
Si t est l'abscisse de B(t;t²), le centre du cercle J a pour coordonnées (0;t²+0,5)
t doit vérifier JB²=JC² (i) où C(0;c)
\Leftrightarrow t^2+0,25=(t^2+0,5-c)^2 \\ <br />\Leftrightarrow t^2+0,25=t^4+0,25+c^2+t^2-2ct^2-c \\ <br />\Leftrightarrow t^4-2ct^2+c^2-c=0 \Leftrightarrow T^2-2cT+c^2-c=0)
en posant T=t²
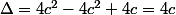
donc
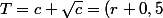^2+r+0,5=r^2+2r+0,75)
, l'autre solution ne convient pas.
Finalement J(0;r²+2r+1,25)
et le rayon du deuxième cercle est JC=
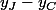
=r+1