Pour aller plus loin avec le premier programme, si on connait le logarithme népérien (log en python),
on peut afficher S-log(n) et faire apparaître une certaine constante mais la convergence est très lente, il faut donner de grandes valeurs à n
Exerice de Maths Python
29 messages
- Page 2 sur 2 - 1, 2
Re: Exerice de Maths Python
human999 a écrit:Ca me donne pleins de chiffres compris entre 1400 et 1500
Mon humble avis, c'est que tu n'as pas compris grand chose au problème et que tu cherches au petit bonheur.
Est-ce que tu as calculé à la main (ou avec un tableur) :
S(1) = 1
S(2) = 1+1/2
S(3) = 1+1/2+1/3
...
Tu verras que la suite S(n) est croissante (facile à démontrer) et qu'elle tend vers +oo (moins intuitif).
Comme elle tend vers +oo, ça veut dire que quelle que soit la valeur A qu'on se donne, on peut trouver un N tel que pour tout n>N, S(n)>A.
Dans ton cas, A=18.
Des valeurs de n telles que S(n)>18, il y en a une infinité.
On te demande de trouver la plus petite :
De sorte que
Re: Exerice de Maths Python
D'après ce que j'ai compris je dois d'abord trouver S à l'aide d'un algorithme puis n à l'aide d'un autre algorithme mais le problème c'est que je suis obligée de le faire avec un algorithme mais quand je tape sur le logiciel ça marche pas
Re: Exerice de Maths Python
Pour le 1er algorithme, ce qua écrit chan79 doit faire l'affaire
Pour cet algo, tu entres une valeur n, il te donne S(n)=1+1/2+...+1/n
Pour le 2ème algo, il faut écrire un truc avec un while : tant que S(n)<18, on continue. Dès que S(n)>18 on arrête et on affiche la valeur de n correspondante (ce que j'ai appelé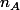 dans mon précédent message).
dans mon précédent message).
chan79 a écrit:n=int(input("saisir la valeur de n:"))
S=0
for i in range(1,n+1):
S=S+1/i
print("S(",n,")=",S)
Pour cet algo, tu entres une valeur n, il te donne S(n)=1+1/2+...+1/n
Pour le 2ème algo, il faut écrire un truc avec un while : tant que S(n)<18, on continue. Dès que S(n)>18 on arrête et on affiche la valeur de n correspondante (ce que j'ai appelé
Re: Exerice de Maths Python
envoie une image de ton algo
J'espère que tu as compris qu'on ajoute 1/n à chaque fois
S+=n signifie que tu ajoutes n à S
S+=1/n signifie que tu ajoutes 1/n à S
J'espère que tu as compris qu'on ajoute 1/n à chaque fois
S+=n signifie que tu ajoutes n à S
S+=1/n signifie que tu ajoutes 1/n à S
Re: Exerice de Maths Python
Bonjour,
ça "marche" parfaitement au contraire! L'algorithme effectue le travail demandé : il affiche la valeur du plus petit entier n tel que 1+1/2+1/3+....+1/n dépasse 18, et cet entier vaut 36865413
ça "marche" parfaitement au contraire! L'algorithme effectue le travail demandé : il affiche la valeur du plus petit entier n tel que 1+1/2+1/3+....+1/n dépasse 18, et cet entier vaut 36865413
Re: Exerice de Maths Python
Deux faits sont observés et demandent explications :
- un tel entier existe (ben oui, quand on ajoute une infinité de trucs de plus en plus petits, il n'est pas sûr qu'on arrive à dépasser une valeur donnée. En fait ça dépend de la vitesse à laquelle les trucs deviennent plus petits).
- cet entier est quand même très grand! Un Nombre n à 8 chiffres pour que la somme dépasse 18, et si un élève est né le 31/12, pour que la somme dépasse 43, ça ferait un nombre très grand... (à 18 chiffres!) je ne vois pas comment une boucle while pourrait effectuer autant d'opérations (de l'ordre du milliard de milliard !) en un temps raisonnable...
Pour comprendre cela, il faut creuser un peu la question : cette somme des inverses des entiers est connue sous le nom de "série harmonique", et dire que cette somme "dépasse n'importe quelle valeur fixée, tant qu'on va assez loin" se dit "la série harmonique diverge".
Pour une exposition rigoureuse des faits, voir par exemple ici :
https://images.math.cnrs.fr/Serie-harmo ... laire.html
- un tel entier existe (ben oui, quand on ajoute une infinité de trucs de plus en plus petits, il n'est pas sûr qu'on arrive à dépasser une valeur donnée. En fait ça dépend de la vitesse à laquelle les trucs deviennent plus petits).
- cet entier est quand même très grand! Un Nombre n à 8 chiffres pour que la somme dépasse 18, et si un élève est né le 31/12, pour que la somme dépasse 43, ça ferait un nombre très grand... (à 18 chiffres!) je ne vois pas comment une boucle while pourrait effectuer autant d'opérations (de l'ordre du milliard de milliard !) en un temps raisonnable...
Pour comprendre cela, il faut creuser un peu la question : cette somme des inverses des entiers est connue sous le nom de "série harmonique", et dire que cette somme "dépasse n'importe quelle valeur fixée, tant qu'on va assez loin" se dit "la série harmonique diverge".
Pour une exposition rigoureuse des faits, voir par exemple ici :
https://images.math.cnrs.fr/Serie-harmo ... laire.html
29 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 68 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :


