Bonjour,
J’ai un contrôle sur les suites et la dérivation et je ne comprends pas tout,
Ci dessous 2 questions auxquelles je n’arrive pas à répondre
1)« Soit u la suite définie pour tout n appartient à N par Un=-2n^2+n
Par la méthode de votre choix ( calcul de Un+1 -Un ou bien étude du sens de variation de f telle que Un= f(n) ), établir le sens de variation de u «
« 2)soit v la suite définie par V0=5 et pour tout entier n>=0, Vn+1 = Vn-2n
Calculer Vn+1-Vn puis établir le sens de variation de la suite v «
Merci d’avance !
Exercice Suites première
6 messages
- Page 1 sur 1
Re: Exercice Suites première
Bonjour,
Pas de dérivation dans ce sujet.
La suite) est donc définie par
est donc définie par 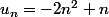
et la suite (v_n) est définie par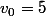 et
et 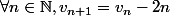
Question 1, pour) : quelles sont les différentes méthodes que vous avez vu en cours pour étudier le sens de variation d'une suite ?
: quelles sont les différentes méthodes que vous avez vu en cours pour étudier le sens de variation d'une suite ?
Question 2, pour) : avez-vous calculé
: avez-vous calculé 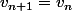 ? Si oui qu'est-ce qu'on en déduit ?
? Si oui qu'est-ce qu'on en déduit ?
Remarque générale : au-delà des "formules", la notion de variation est avant tout du français. Donc ici, même sans avoir connaissance du cours, le bon sens doit vous mettre sur la voie.
Pas de dérivation dans ce sujet.
La suite
et la suite (v_n) est définie par
Question 1, pour
Question 2, pour
Remarque générale : au-delà des "formules", la notion de variation est avant tout du français. Donc ici, même sans avoir connaissance du cours, le bon sens doit vous mettre sur la voie.
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Exercice Suites première
Bonjour, pour la 1- le problème c’est que je n’ai pas vraiment eu de cours dessus avec le confinement donc je ne sais pas trop, j’ai utilisé la première (Un+1-Un) mais je ne suis pas sure du résultat
J’ai fait :
-2(n+1)^2 + (n+1) -(-2n^2 + ´)
= -2n^2+1 +2n^2+1
=2
2>0 donc u est croissant
Pour la 2 j’avais calculé Vn+1 - Vn et ça donnait -2, mais encore une fois je ne suis pas sure du tout
J’ai fait :
-2(n+1)^2 + (n+1) -(-2n^2 + ´)
= -2n^2+1 +2n^2+1
=2
2>0 donc u est croissant
Pour la 2 j’avais calculé Vn+1 - Vn et ça donnait -2, mais encore une fois je ne suis pas sure du tout
Re: Exercice Suites première
oooop a écrit: j’ai utilisé la première (Un+1-Un)
C'est l'une des démarches possibles.
oooop a écrit:-2(n+1)^2 + (n+1) -(-2n^2 + ´)
vous voulez écrire je pense
oooop a écrit:= -2n^2+1 +2n^2+1
Comment obtenez-vous ce résultat ? Détaillez ce calcul car il y a des erreurs
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Exercice Suites première
J’ai refait le calcul et j’obtiens
-2(n+1)(n+1) + (n+1)+ 2n^2 -n
= -2(n^2+n+1)+(n+1)+2n^2 -n
Ce qui est encore + bizarre, je ne comprends pas comment faire honnêtement
(Sinon j’avais fait n+1-n=1, vous demandiez)
-2(n+1)(n+1) + (n+1)+ 2n^2 -n
= -2(n^2+n+1)+(n+1)+2n^2 -n
Ce qui est encore + bizarre, je ne comprends pas comment faire honnêtement
(Sinon j’avais fait n+1-n=1, vous demandiez)
Re: Exercice Suites première
oooop a écrit:J’ai refait le calcul et j’obtiens
-2(n+1)(n+1) + (n+1)+ 2n^2 -n
= -2(n^2+n+1)+(n+1)+2n^2 -n
Pou commencer, vous devez connaître vos identités remarquables : la première est
Mais admettons : vous les avez oubliées (c'est pas bien, mais bon). Vous écrivez
Et vous faites une erreur de développement. Il faut revoir le mécanisme de développement :
Enfin, tant que vous ne maîtrisez pas bien ces techniques, vous devez : (1) en faire, en faire, en faire, tous les jours pendant 5 à 10 minutes en prenant des exercices un peu partout (vous verrez, c'est comme quand vous avez appris à marcher : au bout d'un certain moment vous saurez faire sans y penser) et (2) vérifier en prenant des exemples.
Ainsi : en prenant n=5 alors n+1=6 et (n+1)(n+1)=36, mais 5²+5+1=31 : cela indique qu'il y a une erreur.
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 61 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
