étude de signe d'une fonction

[polomaf]

Bonjour, je bloque un peu sur une étude de signe et j'aurais besoin d'aide...

f(x)=e^(2x)-3e^(x)+2
je veux donc trouver la valeur de x pour que f(x) soit égale à 0
ai-je le droit de procéder ainsi ? :
e^(2x)-3e^(x)+2=0
e^(2x)-3e^(x) +3 =1
ln(e^(2x))- (ln(3)+ln(e^x)) + ln(3) = ln(1)
Je ne suis pas sûr de la véracité de la ligne du dessus, j'ai fait cela car je veux me débarrasser de la forme exponentielle, seulement si je passe le 2 à droite de l'équation, je ne pourrai pas utiliser ln car 2 sera devenu -2.
La deuxième chose qui me bloque est que je ne sais pas si je peux passer de -3e^(x) à -(ln(3)+ln(e^(x))
Merci.

[Pisigma]

Bonjour,

si tu poses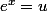 tu obtiens une équation du second degré en u

d'où 2 valeurs de u et de

[polomaf]

Merci !

[Pisigma]

De rien