Equation
21 messages
- Page 1 sur 2 - 1, 2
Equation
Bonjour à tous je n'arrive pas à résoudre l'équation suivante venant d'un problème sur les fonctions
La question est : Quelles sont les antécédents de 0 par la foction f(x)
Or f(x) = x²-x-6
Donc l'équation est x²-x-6 = 0 mas je n'arrive pas à la résoudre merci beaucoup
La question est : Quelles sont les antécédents de 0 par la foction f(x)
Or f(x) = x²-x-6
Donc l'équation est x²-x-6 = 0 mas je n'arrive pas à la résoudre merci beaucoup
Re: Equation
Bonjour
Le professeur de façon générale admettra ta réponse si elle est justifiée par rapport à ce que tu as vu en classe (ou exceptionnellement si tu a appris des trucs par toi même...)
Néanmoins c'est difficile de répondre à ta question car ici il s'agit de savoir résoudre une équation polynomiale de degré 2. Le tout est d'abord de savoir si tu as étudié cela en classe.
(Comme par exemple as-tu appris qu'une telle équation admet au plus 2 solutions (dans \R).
Le professeur de façon générale admettra ta réponse si elle est justifiée par rapport à ce que tu as vu en classe (ou exceptionnellement si tu a appris des trucs par toi même...)
Néanmoins c'est difficile de répondre à ta question car ici il s'agit de savoir résoudre une équation polynomiale de degré 2. Le tout est d'abord de savoir si tu as étudié cela en classe.
(Comme par exemple as-tu appris qu'une telle équation admet au plus 2 solutions (dans \R).
Re: Equation
Je viens de finir ma seconde et je n'est donc pas appris cette méthode pour la résoudre
Re: Equation
Bonjour,
Tu verras donc en première la méthode générale de résolution des équations du second degré.
Sinon, quelques règles toujours vraies : quand on cherche à résoudre une équation, on commence par comparer à zéro (ce qui est le cas ici), puis on cherche à factoriser : car un produit est nul ssi l'un des facteurs est nul.
Donc sans savoir la méthode de résolution du second degré, on peut chercher à factoriser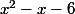 . Malheureusement ici, il n'y a pas de mise en facteur immédiate ni d'identité remarquable.
. Malheureusement ici, il n'y a pas de mise en facteur immédiate ni d'identité remarquable.
Une façon de faire est alors de chercher s'il n'y a pas des valeurs particulières qui annulent le polynôme. On cherche des valeurs simples : (rarement au-delà). Or ici, on voit que -2 est une racine car
(rarement au-delà). Or ici, on voit que -2 est une racine car ^2-(-2)-6=0) .
.
D'où ce résultat : puisque -2 et une racine, le polynôme pourrait s'écrire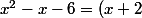(ax+b)) , car avec
, car avec 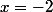 , il est nul, donc l'un des facteurs s'annule pour
, il est nul, donc l'un des facteurs s'annule pour 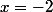 , un tel facteur peut être
, un tel facteur peut être 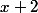 (en fait, la théorie des polynômes garantit que cela va marcher...)
(en fait, la théorie des polynômes garantit que cela va marcher...)
Il n'y a alors plus qu'à développer pour trouver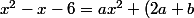x+2b) et cela donne
et cela donne 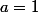 (pour avoir
(pour avoir  ) puis
) puis 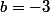 (pour avoir
(pour avoir 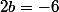 ).
).
On vérifie (pour éviter une bête erreur de calcul) que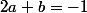 et on obtient finalement
et on obtient finalement 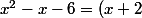(x-3)) ce qui donne la seconde racine :
ce qui donne la seconde racine : =0) ssi
ssi 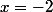 ou
ou 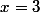
Un tel déroulement est tout à fait admissible en seconde (même si c'est quand même réservé "aux bons matheux" de la classe). Le seul point "hors programme" est l'affirmation que la factorisation va aboutir, mais ici on ne l'affirme pas, on se contente "d'espérer trouver et
et  "
"
Tu verras donc en première la méthode générale de résolution des équations du second degré.
Sinon, quelques règles toujours vraies : quand on cherche à résoudre une équation, on commence par comparer à zéro (ce qui est le cas ici), puis on cherche à factoriser : car un produit est nul ssi l'un des facteurs est nul.
Donc sans savoir la méthode de résolution du second degré, on peut chercher à factoriser
Une façon de faire est alors de chercher s'il n'y a pas des valeurs particulières qui annulent le polynôme. On cherche des valeurs simples :
D'où ce résultat : puisque -2 et une racine, le polynôme pourrait s'écrire
Il n'y a alors plus qu'à développer pour trouver
On vérifie (pour éviter une bête erreur de calcul) que
Un tel déroulement est tout à fait admissible en seconde (même si c'est quand même réservé "aux bons matheux" de la classe). Le seul point "hors programme" est l'affirmation que la factorisation va aboutir, mais ici on ne l'affirme pas, on se contente "d'espérer trouver
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Equation
Si j'ai bien compris ta réponse, Léo, tu dis que la résolution d'une équation du second degré n'est pas au programme de fin de seconde. Aussi, je me demande pourquoi tu crains que le professeur n'admettrait pas que tu donnes la solution " hors programme " vu que tu n'es pas censé avoir acquis la méthode de résolution.
Je ne sais pas si je me fais bien comprendre.....
Je ne sais pas si je me fais bien comprendre.....
Re: Equation
Pour te persuader qu'il n'y a que 2 solutions, tu peux esquisser la courbe sur une graphique, tu t'en rendras compte rapidement.
Re: Equation
Salut !
Sinon la méthode générale consiste à exprimer le début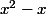 de
de 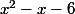 comme le début de l'identité remarquable "
comme le début de l'identité remarquable "^2=a^2+2ab+b^2) ", où l'on prend
", où l'on prend  et
et  . On aura alors :
. On aura alors :
^2-b^2=\left( x - \frac 1 2 \right)^2 - \left( - \frac 1 2 \right)^2 =\left( x - \frac 1 2 \right)^2 - \frac 1 4) .
.
Ainsi résoudre revient à résoudre
revient à résoudre ^2 - \frac 1 4 -6 =0) , c'est-à-dire
, c'est-à-dire ^2 - \frac{25} 4 =0) . En voyant
. En voyant  comme le carré de
comme le carré de  , on se retrouve avec une identité remarquable "
, on se retrouve avec une identité remarquable "(A+B)) ", où
", où  et
et  . Ce faisant, on a :
. Ce faisant, on a :
^2 - \frac{25} 4 = A^2-B^2 = (A-B)(A+B)= \left( x - \frac 1 2 - \frac 5 2 \right)\left( x - \frac 1 2 + \frac 5 2 \right) = \left( x - \frac 6 2 \right)\left( x + \frac 4 2 \right) = (x-3)(x+2)) .
.
Par conséquent, résoudre^2 - \frac{25} 4 =0) équivaut à résoudre
équivaut à résoudre (x+2)=0) . D'où la conclusion.
. D'où la conclusion.
En espérant t'avoir éclairé bien que je suis conscient que ça puisse ne pas être évident au premier regard.

P.S. : Cette méthode est généralisable mais il peut arriver qu'il n'y ait pas de solution, par exemple l'équation , n'a pas de solution dans
, n'a pas de solution dans  .
.
Sinon la méthode générale consiste à exprimer le début
Ainsi résoudre
Par conséquent, résoudre
En espérant t'avoir éclairé bien que je suis conscient que ça puisse ne pas être évident au premier regard.
P.S. : Cette méthode est généralisable mais il peut arriver qu'il n'y ait pas de solution, par exemple l'équation
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Re: Equation
en seconde, il y a bien un cours "meilleur forme".
on te demandes de démonter que des écritures de f(x) sont en fait les même
et ensuite tu choisis celle qui permet de résoudre l'équation
f(x)=x²-x-6
est équivalent à
f(x)= (x-1/2)² -25/4 <- qui est donné en seconde ou fortement inspiré
f(x)=0 est don équivalent à (x-1/2)² -25/4=0
équivaut à (x-1/2)²= 25/4
(x-1/2)²= (5/2)²
x-1/2 = 5/2 soit x-1/2=-5/2
...
on te demandes de démonter que des écritures de f(x) sont en fait les même
et ensuite tu choisis celle qui permet de résoudre l'équation
f(x)=x²-x-6
est équivalent à
f(x)= (x-1/2)² -25/4 <- qui est donné en seconde ou fortement inspiré
f(x)=0 est don équivalent à (x-1/2)² -25/4=0
équivaut à (x-1/2)²= 25/4
(x-1/2)²= (5/2)²
x-1/2 = 5/2 soit x-1/2=-5/2
...
Re: Equation
Salut,
Je sais pas trop ce qu'on voit en seconde, mais un truc qui me semble possible, c'est qu'on y voit comment faire des "lectures graphiques" sur le tracé d'une courbe, en particulier la lecture des antécédents d'un réel donné.
Est-ce que ça ne pourrait pas être ça qui est attendu : tracé de la courbe avec une calculette, "lecture graphique" des solutions puis éventuellement vérification calculatoire ?
Je sais pas trop ce qu'on voit en seconde, mais un truc qui me semble possible, c'est qu'on y voit comment faire des "lectures graphiques" sur le tracé d'une courbe, en particulier la lecture des antécédents d'un réel donné.
Est-ce que ça ne pourrait pas être ça qui est attendu : tracé de la courbe avec une calculette, "lecture graphique" des solutions puis éventuellement vérification calculatoire ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Equation
Salut,
En 2nde, il y a un chapitre "polynôme du second degré" qui est souvent fait en fin d'année où on voit un théorème donnant les variations des fonctions polynôme du second degré. En particulier, on voit que de telles fonctions sont soit croissantes puis décroissantes (sur un intervalle) ou soit l'inverse. Ce résultat permet de comprendre qu'une équation polynôme du second degré (c'est à dire une équation de la forme ax^2+bx+c=0 avec a non nul) a au plus 2 solutions.
À partir de là, en reprenant l'équation dont il est question, on peut chercher deux solutions en testant (ce qui marche bien ici).
En fait, c'est précisément ce que décrit Ben314 mais la représentation graphique de la fonction polynôme doit être trouvable en 2nde sans utiliser sa calculette.
En 2nde, il y a un chapitre "polynôme du second degré" qui est souvent fait en fin d'année où on voit un théorème donnant les variations des fonctions polynôme du second degré. En particulier, on voit que de telles fonctions sont soit croissantes puis décroissantes (sur un intervalle) ou soit l'inverse. Ce résultat permet de comprendre qu'une équation polynôme du second degré (c'est à dire une équation de la forme ax^2+bx+c=0 avec a non nul) a au plus 2 solutions.
À partir de là, en reprenant l'équation dont il est question, on peut chercher deux solutions en testant (ce qui marche bien ici).
En fait, c'est précisément ce que décrit Ben314 mais la représentation graphique de la fonction polynôme doit être trouvable en 2nde sans utiliser sa calculette.
Pseudo modifié : anciennement Trident2.
Re: Equation
Bonjour,
La mise sous forme canonique d'un polynôme du 2nd degré (méthode de @pascal16) ne te dit rien ?
La mise sous forme canonique d'un polynôme du 2nd degré (méthode de @pascal16) ne te dit rien ?
Re: Equation
Mon professeur de maths est parti en congé maladie à 2 mois de la fin d’année et malheureusement il n’a pas été remplacé
Je n’ai donc pas vu le chapitre sur le polynôme du second degrés
Si je suis censé le savoir, cela explique pourquoi cela est demandé dans un exercice de rentrée en première
Je n’ai donc pas vu le chapitre sur le polynôme du second degrés
Si je suis censé le savoir, cela explique pourquoi cela est demandé dans un exercice de rentrée en première
Re: Equation
pascal16 a écrit:forme canonique, c'est du programme de 1er
Bonsoir,
En effet. On utilise la forme canonique en 2nde (et en 3ème) sans le dire pour déterminer le maximum et le minimum d'une fonction polynôme du 2nd degré. Mais beaucoup de profs (la plupart) mettent un nom en 2nde, et même font la mise sous forme canonique.
Modifié en dernier par Pseuda le 27 Aoû 2018, 20:42, modifié 1 fois.
Re: Equation
Léo a écrit:Mon professeur de maths est parti en congé maladie à 2 mois de la fin d’année et malheureusement il n’a pas été remplacé
Je n’ai donc pas vu le chapitre sur le polynôme du second degrés
Si je suis censé le savoir, cela explique pourquoi cela est demandé dans un exercice de rentrée en première
Bonsoir,
C'est embêtant pour toi. Pour résoudre cette équation, il faut savoir :
- mettre sous forme canonique un polynôme du 2nd degré (pas au programme de la 2nde, mais des profs le font) : (x-1/2)^2 - 25/4
- puis factoriser le polynôme (vu en 3ème, approfondi en 2nde) : (x-3)(x+2), en utilisant l'identité remarquable a^2-b^2=(a+b)(a-b)
- puis résoudre l'équation produit (vu en 3ème) : (x-3)(x+2)=0.
Mais en 1ère, tu verras une méthode plus rapide, qui donne directement la formule !
Re: Equation
L’exercice était constitué dans graphique de la fonction f et la question était de retrouver algébriquement les antécédents de 0 par f
21 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 71 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
