Equation racine carré
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Rafifou
- Messages: 3
- Enregistré le: 31 Juil 2018, 18:27
-
 par Rafifou » 31 Juil 2018, 18:39
par Rafifou » 31 Juil 2018, 18:39
Bonjour à tous,
Voila maintenant plusieurs jours que je m'arrache les cheveux sur cette équation:
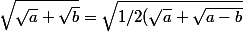+\sqrt{1/2(\sqrt{a}-\sqrt{a-b}}))
Je dois montrer que

est égal à
+\sqrt{1/2(\sqrt{a}-\sqrt{a-b}}))
J'ai essayé d'appliquer les identités remarquables mais sans succès.
Merci d'avance pour votre précieuse aide.
Modifié en dernier par
Rafifou le 31 Juil 2018, 19:35, modifié 6 fois.
-
danyL
- Membre Rationnel
- Messages: 682
- Enregistré le: 03 Jan 2015, 13:29
-
 par danyL » 31 Juil 2018, 18:53
par danyL » 31 Juil 2018, 18:53
pour la forme :
il faut encadrer les expressions de balises tex, il y a un bouton tex pour ça dans l'editeur complet
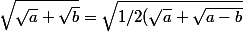+\sqrt{1/2(\sqrt{a}-\sqrt{a-b}}))
pour le fond :
les vrais matheux vont te répondre
![Dan.San :]](https://www.maths-forum.com/images/smilies/8.gif)
mais en attendant, as-tu essayé d'élever au carré les 2 expressions ?
-
Rafifou
- Messages: 3
- Enregistré le: 31 Juil 2018, 18:27
-
 par Rafifou » 31 Juil 2018, 19:07
par Rafifou » 31 Juil 2018, 19:07
Merci beaucoup danyL (étant nouveau sur le forum je n'ai pas encore les bons réflexes.
Et oui, l'élévation au carré n'a pas donné grand chose de mon coté

-
hdci
- Membre Irrationnel
- Messages: 1962
- Enregistré le: 23 Juin 2018, 16:13
-
 par hdci » 31 Juil 2018, 20:12
par hdci » 31 Juil 2018, 20:12
Pourtant en élevant au carré le terme de droite, cela marche.
Notons
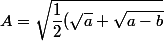+\sqrt{\dfrac{1}{2}(\sqrt{a}-\sqrt{a-b}}))
Alors
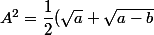+\dfrac{1}{2}(\sqrt a-\sqrt{a-b})+2\cdot\dfrac{1}{2}\sqrt{(\sqrt a+\sqrt{a-b})((\sqrt a-\sqrt{a-b})})
Il y a des simplfications (deux moitiés de racine de a cela fait une seule racine de a à droite, les racines de a-b qui s'annulent, puis une identité remarquable tout à fait à droite qui supprime les racines dans les racines), et cela donne
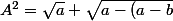})
D'où

Il faut néanmoins s'assurer que toutes les racines ont un sens.
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
-
Rafifou
- Messages: 3
- Enregistré le: 31 Juil 2018, 18:27
-
 par Rafifou » 31 Juil 2018, 20:49
par Rafifou » 31 Juil 2018, 20:49
Merci beaucoup hdci pour cette réponse détaillée et rapide!
Je vais re-travailler tout ça en m'aidant de tes calculs.
-
pascal16
- Membre Légendaire
- Messages: 6663
- Enregistré le: 01 Mar 2017, 12:58
- Localisation: Angoulème : Ville de la BD et du FFA. gare TGV
-
 par pascal16 » 02 Aoû 2018, 13:28
par pascal16 » 02 Aoû 2018, 13:28
Aymanemaysae, la racine d'un produit n'est pas égal au produit des racines dans le cas général
√4 ne vaut pas √(-1/2) √(-8)
par contre, si on dit dès le départ que a≥0 et b≥0 et a≥b, tes équivalences sont justes
-
aymanemaysae
- Habitué(e)
- Messages: 1265
- Enregistré le: 06 Sep 2013, 14:21
-
 par aymanemaysae » 02 Aoû 2018, 13:32
par aymanemaysae » 02 Aoû 2018, 13:32
Bonjour;
Tu as parfaitement raison .
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 62 invités
![Dan.San :]](https://www.maths-forum.com/images/smilies/8.gif)
