Peut-on résoudre ce genre d'équation dans
équation partie entière
19 messages
- Page 1 sur 1
équation partie entière
Bonsoir, j'aimerai savoir comment résoudre une équation avec une partie entière du genre =m, m\in\mathbb{R}.)
Peut-on résoudre ce genre d'équation dans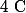 ?
?
Peut-on résoudre ce genre d'équation dans
Ben, vu que E(x)=m signifie (par définition) que m <= x < m+1, résoudre une telle équation, ça revient à résoudre deux inéquations.
Comme la définition de la partie entière contient la notion de relation d'ordre (le <= et le <) et qu'il n'y a pas de "bonne" relation d'ordre sur l'ensemble des complexe, ben on peut pas trop définir "proprement" la notion de partie entière d'un complexe...
Comme la définition de la partie entière contient la notion de relation d'ordre (le <= et le <) et qu'il n'y a pas de "bonne" relation d'ordre sur l'ensemble des complexe, ben on peut pas trop définir "proprement" la notion de partie entière d'un complexe...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Equations et parties entières
Je résume la discussion étant donné que je l'ai déplacée suite à une erreur de rubrique ^^
Dinozzo13 a écrit:Bonsoir, j'aimerai savoir comment résoudre une équation avec une partie entière du genre=m, m\in\mathbb{R}.)
Peut-on résoudre ce genre d'équation dans?
.Ben314 a écrit:Ben, vu que E(x)=m signifie (par définition) que m <= x < m+1, résoudre une telle équation, ça revient à résoudre deux inéquations.
Comme la définition de la partie entière contient la notion de relation d'ordre (le <= et le <) et qu'il n'y a pas de "bonne" relation d'ordre sur l'ensemble des complexe, ben on peut pas trop définir "proprement" la notion de partie entière d'un complexe...
discussion déplacée
Mince je me suis trompé de rubrique, je déplace donc la discussion :
http://maths-forum.com/showthread.php?p=681193#post681193
http://maths-forum.com/showthread.php?p=681193#post681193
Non, ce nest pas bon car E(a)=E(b) n'est pas équivalent à |b-a| |b-a|<1
Par exemple, si a=0.99 et b=1.01 alors |b-a|<1 alors que E(a) n'est pas égal à E(b).
Conclusion, tu peut commencer par résoudre tes deux inéquations, mais tu aura trop de solutions...
P.S. :
Arnaud a fait une faute de frappe dans son post 6, la partie entière de x est l'unique entier n tel que , c'est à dire
, c'est à dire  ou encore
ou encore 
Par exemple, si a=0.99 et b=1.01 alors |b-a|<1 alors que E(a) n'est pas égal à E(b).
Conclusion, tu peut commencer par résoudre tes deux inéquations, mais tu aura trop de solutions...
P.S. :
Arnaud a fait une faute de frappe dans son post 6, la partie entière de x est l'unique entier n tel que
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Cherche pas : à un point virgule prés, ça dit que tout réel admet une partie entière (ce qui, si on ne connait pas la définition précise d'un nombre réel peut être considéré comme une "évidence")Dinozzo13 a écrit:Je ne sais pas ce que cela signifie que R soit archimédien.
Aprés, par rapport à ce qu dit arnaud, l'idé que j'avais, c'est que, pour résoudre E(P(x))=E(Q(x)), si tu commence par résoudre |P(x)-Q(x)|<1, avec un peu de pot tu risque de voir qu'il n'y a qu'un nombre fini (petit ?) d'entiers possible pour E(P(x))=E(Q(x)) et il suffit alors de résoudre pour chacun d'eux.
Bon, de toute façon, c'est le genre d'équation que, à part pour quelques "casse-têtes" j'ai rarement rencontré...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
19 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 72 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
