Equation Parabole passant par trois points

[chan79]

salut
il y a ce résultat
Par quatre points, il passe deux paraboles (sauf cas particuliers)

[GaBuZoMeu]

Ces cas ne sont pas si particuliers que ça ! Combien de paraboles peux-tu faire passer par les quatre points a, b, c, d si d est à l'intérieur du triangle abc ?

[Dattier]

Une petite explication : l'intersection de parabole est convexe (comme intersection de 2 convexes)

Quand on prend d tel que le suggère GBZM on a un problème avec la convexité.

Ce qu'il fallait expliquer.

[Dattier]

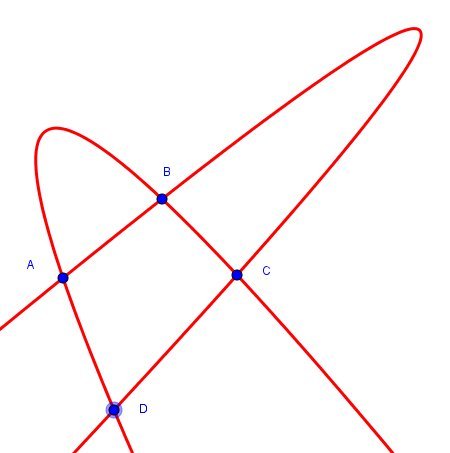
Une petite explication : l'intersection de 2 paraboles est convexe (comme intersection de 2 convexes)

Quand on prend d tel que le suggère GBZM on a un problème avec la convexité.

Ce qu'il fallait expliquer.

[GaBuZoMeu]

Correct, mais je dirais plutôt :
L'"interieur" d'une parabole est strictement convexe. Donc si on prend trois points sur une parabole, il n'y a aucun autre point de la parabole à l'intérieur du triangle dont ils sont les sommets.
Aucune parabole ne peut passer par quatre points dans la configuration que j'ai indiquée. De même pour les ellipses.

[Dattier]

Remarque il en est de même si on choisie les 4 points comme sommets d'un rectangle.

[GaBuZoMeu]

Ça, c'est un "cas particulier" de Chan où les deux paraboles dégénèrent en deux paires de droites parallèles.

[Dattier]

Oui, oui, et le cas dont tu parlais est un "cas particulier" de Chan où les 2 paraboles dégènérent en une lemniscate.

[GaBuZoMeu]

Là, Dattier, ce que tu écris, c'est n'importe quoi !
Une paire de droite est une conique dégénérée. Et dès qu'on perturbe un tant soit peu un des quatre sommets du rectangle, on retrouve bien les deux paraboles.
Par contre, dans le cas où le point d est à l'intérieur du triangle abc, il le sera toujours après une petite perturbation des quatre points et on n'aura toujours aucune parabole passant par les quatre points perturbé.

[Dattier]

Une paire de droite est une conique dégénérée.

Quelle est ta définition d'une parabole dégénéré ou non, alors ?

(voilà ce que je sais sur les paraboles : https://fr.wikipedia.org/wiki/Parabole
là dedans pas de paires de droites paraboles)

[GaBuZoMeu]

Une conique est une courbe donnée par une équation du second degré :

qui peut se mettre sous forme matricielle


La conique est non dégénérée quand le rang de est 3.
La classification affine des coniques réelles non dégénérées peut se voir sur la signature de et de la matrice de la partie quadratique de l'équation :
Signature de : (3,0) ou (0,3). Conique non dégénérée vide.
Signature de : (2,1) ou (1,2). Ce sont les coniques propres. Parmi elles, les ellipses (signature de : (2,0) ou (0,2) respectivement), les hyperboles (signature de : (1,1)) et les paraboles (signature de : (1,0) ou (0,1) respectivement).

Les coniques dégénérées avec de rang 2 sont les paires de droites distinctes. La aussi, on peut classer suivant la signature de Q : ce qui correspond aux ellipses sont les paires de droites complexes conjuguées, aux hyperboles les paires de droites réelles sécantes, aux paraboles les paires de droites parallèles.

[chan79]

Ces cas ne sont pas si particuliers que ça ! Combien de paraboles peux-tu faire passer par les quatre points a, b, c, d si d est à l'intérieur du triangle abc ?

Je précise. Par 4 points, il passe au maximum deux paraboles.
Ce qui est intéressant, c'est de les construire.

[GaBuZoMeu]

0, en fait. Ou alors tu comptes les paraboles complexes conjuguées ?

[GaBuZoMeu]

Bon, moi je n'ai pas le droit de modifier mes messages une fois postés dans ce forum.

[Pierre256]

Bonsoir,
Je me répète :
Evidemment, je réagis un peu indépendamment de cet exercice niveau lycée, mais il me parait important de le rappeler. Donc, pardon pour cette intervention parasite.
Encore pardon d'avoir rappelé une caractéristique très importante et très utilisée de la parabole.

[Dattier]

Par quatre points, il passe deux paraboles (sauf cas particuliers)

On se place dans une feuille carré Ca de côté l'unité, avec un tirage uniforme.

La probabilité qu'il soit dans la configuration de GBZM est de :



ce qui n'est pas nul.

[Dattier]

Par quatre points, il passe deux paraboles (sauf cas particuliers)

On se place dans une feuille carré Ca de côté l'unité, avec un tirage uniforme.

La probabilité qu'il soit dans la configuration de GBZM est de :



ce qui n'est pas nul.

Mais c'est du chipotage ou de l'ultramaths...

[aviateur]

Pour mémoire, bon nombre de logiciels dessinent les courbes de niveau par une succession d'arcs de parabole. On peut aussi utiliser cette méthode pour dessiner des arcs de cercle etc. .

J'ai 2 questions
C'est compliqué un arc de cercle pour l'approximer par une parabole?

Ensuite,
un ingénieur qui veut construire une attraction de fête foraine,comme par exemple une montagne russe, et, si
pour simplifier le problème, on va supposer qu'une partie de la trajectoire est dans le plan, alors il va contruire cette trajectoire avec des arcs de parabole?

[GaBuZoMeu]

Ce fil part dans tous les sens et s'éloigne du lycée. poursuivons gaiement.

Chan79 parle de la construction des paraboles passant par 4 points A, B C, D, quand il veut bien y en avoir. Je montre ici une façon de construire les directions des axes de ces paraboles ; ce sont les directions des droites rouges sur le dessin :



Explication de construction : les directions des axes sont les points fixes de l'involution sur la droite de l'infini donnée par le faisceau de coniques passant par les quatre points A, B, C, D (c'est l'involution qui échange les deux points d'intersection d'une conique du faisceau avec la droite de l'infini). On ramène cette involution sur le cercle circonscrit au triangle ABC par la projection de centre A. L'involution sur le cercle échange les points B et B' (deuxième intersection du cercle avec la parallèle à (CD) passant par A) et les points C et C' (deuxième intersection du cercle avec la parallèle à (BD) passant par A). Le point de Frégier F de cette involution est l'intersection de (BB') et (CC'), et les directions des axes sont données par les droites joignant A aux points de tangence des tangentes au cercle issues de F.
Quand les quatre points ne sont pas les sommets d'un quadrilatère convexe, le point de Frégier F est à l'intérieur du cercle et la construction se casse la figure.

Une fois qu'on a quatre points de la parabole et la direction de son axe, la construction de la parabole est routinière.

[Pierre256]

Bonjour,

C'est compliqué un arc de cercle pour l'approximer par une parabole?

Compliqué, pas vraiment, encore faut-il faire le bon test pour s'arrêter. Il ne faut pas oublier que en matière de dessin informatique, on ne sait faire que des segments de droite, c'est à dire d'aller d'un point à un autre et que quel que soit la façon dont on regarde le problème une courbe sera toujours dessinée par un polygone. Ceci était absolument vrai avec les traceurs à plume. Maintenant, avec la méthode raster, la méthode peut être un peu différente, mais je n'en suis pas tellement sûr.
D'autre part, il est beaucoup plus économique de faire une division par 2 que de calculer 2 lignes trigonométriques.

un ingénieur qui veut construire une attraction de fête foraine,comme par exemple une montagne russe, et, si
pour simplifier le problème, on va supposer qu'une partie de la trajectoire est dans le plan, alors il va contruire cette trajectoire avec des arcs de parabole?

Pour les attractions foraines, si on veut que les clients soient secoués, c'est sûr qu'il vaudra mieux choisir des arcs de cercle, par contre, en ferroviaire (train et métro) on utilise la parabole. En routier, c'est plutôt la clothoïde.

Peux-tu me dire pourquoi cela te gène qu'on utilise la parabole plutôt que le cercle ?