Bonjour, j'ai un devoir de math' où il m'est demander de construire un triangle ABC dans un repère orthonormé et de placer les milieux des trois cotés. Il m'est ensuite demander de calculer en unité de longueur les trois cotés puis de les déduire en centimètre. Ce qui ne m'a pas vraiment posé de problème, mais là il m'est demandé :
Déterminer les équations des médianes puis les coordonnées de G le centre de gravité. Vérifié que les 3 médianes sont concourante en G et que G et bien la où on l'attend soit aux tiers de chaque médianes à partir du milieu de segment.
Donnés obtenus dans l'énoncé et grace aux questions précédentes :
A(8;56) B(-60;5) C(52;-61)
AB(68;51) AC(44;117) BC(112;66)
Merci d'avance.
Equation de Mediane, coordonnée dans un repère ...
9 messages
- Page 1 sur 1
Bonjour
les coordonnées du milieu :
on ajoute les 2 coordonnées et on divise par 2 :
abscisse du milieu = (somme des 2 abscisses )/2
ordonnée : pareil
tu détermines les 3 milieux
la médiane passe par un sommet et le milieu du côté opposé
A est un sommet
A' est le milieu opposé
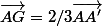
tu peux trouver les coordonnées de G
tu peux trouver l'équation de la droite AA'
et BB'
et CC'
chercher les points d'intersection 2 à 2
vérifier qu'ils sont les mêmes et que c'est G
les coordonnées du milieu :
on ajoute les 2 coordonnées et on divise par 2 :
abscisse du milieu = (somme des 2 abscisses )/2
ordonnée : pareil
tu détermines les 3 milieux
la médiane passe par un sommet et le milieu du côté opposé
A est un sommet
A' est le milieu opposé
tu peux trouver les coordonnées de G
tu peux trouver l'équation de la droite AA'
et BB'
et CC'
chercher les points d'intersection 2 à 2
vérifier qu'ils sont les mêmes et que c'est G
bonsoir,
A(8;56) B(-60;5) C(52;-61)
tu connais les coordonnées de 2 points des médianes, la droite est de forme y=ax+b
par exemple pour (AA')
tu as A(8;56)-->56=a(8)+b
tu peux caculer A'(xb+xc/2;ya+yb/2)
--->(ya+yb)/2=a*(xb+xc)/2 + b
tu as ainsi un système de 2 équations à 2 inconnues
G est le point de concours des médianes
si les droites sont concourantes, elles ont un point commun, écris donc que l'équation de droite de (AA') = l'équation de droite de (BB')= l'équation de droite de (CC')
calcule A'G
A'G²=(xg-xa')²+(yg-ya')²
A(8;56) B(-60;5) C(52;-61)
tu connais les coordonnées de 2 points des médianes, la droite est de forme y=ax+b
par exemple pour (AA')
tu as A(8;56)-->56=a(8)+b
tu peux caculer A'(xb+xc/2;ya+yb/2)
--->(ya+yb)/2=a*(xb+xc)/2 + b
tu as ainsi un système de 2 équations à 2 inconnues
G est le point de concours des médianes
si les droites sont concourantes, elles ont un point commun, écris donc que l'équation de droite de (AA') = l'équation de droite de (BB')= l'équation de droite de (CC')
calcule A'G
A'G²=(xg-xa')²+(yg-ya')²
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 158 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
