équation fonctionnelle

[Pseuda]

en posant g(x)=f(f(x)
en remplaçant y par 0 dans l'équation donnée, on arrive à g(1)=0
en remplaçant x par 0:
f(y)=f(-y)+g(1)
f(y)=f(-y)
f est paire
g est paire aussi

avec y =1 dans l'équation de départ
f(x+1)=f(x-1)+g(1-x)
en remplaçant x par x+1 dans l'égalité précédente:
f(x+2)=f(x)+g(x)
en remplaçant x par -x dans l'égalité précédente et avec les parités de f et g
f(x-2)=f(x)+g(x)
donc f(x+2)=f(x-2)
or f(x+2)=f(x-2)+g(1-2x)
donc g(1-2x)=0
donc g=0
il s'en suit que f(x+y)=f(x-y)
soit deux nombres a et b
si on pose x=(a+b)/2 et y=(a-b)/2
f(x+y)=f(x-y) donne f(a)=f(b)
f est constante
f(f(1))=0 donc f=0

Bravo, et merci beaucoup ! C'est très clair.

Du coup, l'intérêt de ce problème en 1eS (ils ne connaissent pas la dérivation) me paraît un peu décalé.

[Pseuda]

S'il y a des solutions autres que la fonction nulle, alors elle ne sont dérivable nulle part (sauf éventuellement en 0).
Et je ne pense pas que tu arrive à "fabriquer" une fonction nulle part dérivable en partant simplement de la fonction "partie entière".

Merci. Effectivement, alors, la fonction ne peut pas se composer seulement de la fonction partie entière.

[Ben314]

Très jolie solution.
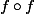
Sinon, s'il y en a qui veulent chercher "plus loin", perso, comme le me faisait c..., j'étais parti sur le fait que, vu que ne dépend que du produit xy on a :
(pour tout non nul).
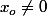
En supposant dérivable en un point on montre relativement facilement que où et sont deux constantes.
Peut-on montrer que sans hypothèse de régularité ?