Ensemble de définition

par **sue** » 02 Jan 2007, 10:20

Bonjour ,

je ne uis pas sûre de l'ensemble de définition de cette fonction définie par :

avec

je trouve

est-ce juste ?

MERCI :we:

par **sue** » 02 Jan 2007, 11:38

je sais que vous avez la flemme de faire le calcul , mais c la première question de mon exo , toute l'étude la fonction repose sur

.
et ça me dérange vraiment de ne pas pouvoir faire ça avec certitude :triste: , j'ai un DS de 4h aprés les vacances et c'est la moindre des choses qu'on peut faire .

alors si qqn pourrait comfirmer ou infirmer ma réponse ça sera sympa .

par **rene38** » 02 Jan 2007, 13:27

Bonjour

Sans avoir fait tout le calcul,
- la définition pour x>=-1 ne pose pas problème.

- pour x1 (ce qui semble bien réalisé pour x=-2 par exemple)
donc partie à revoir.

par **sue** » 02 Jan 2007, 13:53

salut , enfin qqn qui répond :we:

pour x 1 soit u(x)> 1 (j'ai vérifié que u(x)>0) soit

--) (

et x<-1 ) donc

et pour

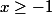
on a

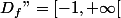
soit

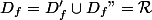
non ? :hein:

par **rene38** » 02 Jan 2007, 15:48

Je n'ai pas vérifié tes calculs mais le résultat est exact.

par **sue** » 02 Jan 2007, 16:03

ok , merci bien à vous :we:

j'ai une autre question svp ,
aprés on me demande de calculer les limites aux bornes de Df
je trouve 0 en +oo et 1+pi/2 en -oo .

par **sue** » 02 Jan 2007, 17:35

pourriez-vous me répondre ?

merci

Ensemble de définition

ensemble de définition

Qui est en ligne