bonjour je n'arrive pas à trouver le domaine de def de:
ln(3x+2xe^(x)-xe^(2x))
Si vous pouvez m'aider merci
Ln domaine de def
8 messages
- Page 1 sur 1
Re: ln domaine de def
Salut !
Cette expression est définie si et seulement si .
.
Or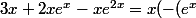^2+2e^{x}+3)) donc sachant que
donc sachant que ^2+2e^{x}+3)>0) équivaut à dire que :
équivaut à dire que :
 et
et ^2+2e^{x}+3>0]) ou
ou  et
et ^2+2e^{x}+3<0]) ,
,
détermine suivant les valeurs de le signe de l'expression
le signe de l'expression ^2+2e^{x}+3) .
.
Tu pourras commencer par étudier le signe du trinôme et remarquer que
et remarquer que ^2+2e^{x}+3 = -t^2+2t+3) , en posant
, en posant 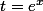 .
.
Cette expression est définie si et seulement si
Or
détermine suivant les valeurs de
Tu pourras commencer par étudier le signe du trinôme
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Re: ln domaine de def
je trouve:
en posant X=e^x
-X^2+2X+3>0
Puis, X=-1 donc impossible ET X=3
Soit en remplaçant x=ln 3
Donc il faut que x>ln 3
en posant X=e^x
-X^2+2X+3>0
Puis, X=-1 donc impossible ET X=3
Soit en remplaçant x=ln 3
Donc il faut que x>ln 3
Re: ln domaine de def
Salut, On obtient grâce au trinôme que c'est positif sur [-1;3] soit[-1;ln3]
Or on a aussi x>0 donc Df est ] 0 ; ln3 [
Or on a aussi x>0 donc Df est ] 0 ; ln3 [
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 70 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
