Divisibilité par 3

[MATRIX02]

Bonjour,
Je sèche sur 2 questions d'un DM.
Énoncé :
n entier naturel non nul,
1) On suppose que n est pair. Montrer que 3 est un diviseur de 2^n -1

2)Soit An = 2^(2^n+1) + 2^(2^n) + 1, en utilisant le 1), justifier que An est divisible par 3.

Comment commencer ?
Merci

[zygomatique]

Bonjour,
Je sèche sur 2 questions d'un DM.
Énoncé :
n entier naturel non nul,
1) On suppose que n est pair. Montrer que 3 est un diviseur de 2^n -1

2)Soit An = 2^(2^n+1) + 2^(2^n) + 1, en utilisant le 1), justifier que An est divisible par 3.

Comment commencer ?
Merci

montrer que est multiple de 3 pour n pair équivaut à montrer que est multiple de 3 pour tout n

ça se fait par récurrence ....

[Tiruxa]

montrer que est multiple de 3 pour n pair équivaut à montrer que est multiple de 3 pour tout n

ça se fait par récurrence ....

Bonsoir,

ou bien sans récurrence en utilisant



Puisque a=4 et b= 1 , a-b=3 d'où la divisibilité par 3.

[MATRIX02]

montrer que est multiple de 3 pour n pair équivaut à montrer que est multiple de 3 pour tout n

ça se fait par récurrence ....

J'ai mis :
héredité : il existe k tel que

donc :

k appartient à N donc (An + 1) est vraie, on a donc montré par récurrence que
est divisible par 3 pour tout n appartenant à N

[paquito]

2^{2n}-1 multiple de 3 pour tout n donne en termes de congruences: 2^{2n}=1 [3]

Or:
2^{0}=1 [3]
2^{2}=1 [3]; donc si par hypothèse de récurrence tu suppose pour un entier n

2^{2n}=1 [3]; comme tu as
2^{2}=1 [3], en faisant le produit, tu obtiens

2^{2n+2}=1 [3], et donc, tu établit ton résultat par récurrence.

[MATRIX02]

j'ai pas vu la congruence !
je demande juste si ma réponse au 1) est bonne et une aide pour commencer le 2)
merci.

[paquito]

Je suppose que ;

on a , donc pour , ça ne marche pas. Sinon est pair, aussi, donc on a:


; donc

Conclusion: est un multiple de pour

[zygomatique]

j'ai pas vu la congruence !
je demande juste si ma réponse au 1) est bonne et une aide pour commencer le 2)
merci.

non .... car tu ne sais pas calculer ....

[zygomatique]

Je suppose que ;

on a , donc pour , ça ne marche pas. Sinon est pair, aussi, donc on a:


; donc

Conclusion: est un multiple de pour

super !!! c'est bien tu sais faire .... mais instruire tu sais ?

:mur:

[paquito]

j'ai pas vu la congruence !
je demande juste si ma réponse au 1) est bonne et une aide pour commencer le 2)
merci.

Si tu n'as pas vu les congruences, tu peux replacer 2^n-1=3k par 2^n=3k+1.

[paquito]

super !!! c'est bien tu sais faire .... mais instruire tu sais ?

:mur:

Matrix n'a pas vu les congruences; ça lui donnera peut être envie d'en savoir plus; quand à instruire ça ne peut pas se limiter à donner de vagues indications, c'est aussi parfois donner un modèle, surtout quand le problème a une apparence déroutante; comment avons nous appris, nous? en jouant aux devinettes?

[zygomatique]

Matrix n'a pas vu les congruences; ça lui donnera peut être envie d'en savoir plus; quand à instruire ça ne peut pas se limiter à donner de vagues indications, c'est aussi parfois donner un modèle, surtout quand le problème a une apparence déroutante; comment avons nous appris, nous? en jouant aux devinettes?

j'ai appris en pensant et en appliquant correctement les règles de calcul ou des raisonnements (par récurrence par exemple)

supposons multiple de 3 pour n pair

alors

alors l'hypothèse de récurrence et la propriété " si a et b sont multiples de c alors a + b est multiple de c" permettent de conclure ...


et il est à noter qu'une lecture attentive de l'énoncé (mais on m'a aussi appris à lire ... correctement) impose la récurrence de 2 en 2 puisqu'on dit que n est pair ....

et c'est le pourquoi de mon premier post ... pour revenir à une récurrence "normale"

de toute façon donner une réponse complète n'est pas de l'instruction .... et laisse l'étudiant dans l'illusion de l'apprentissage ....


ensuite avant d'aller voir plus loin on peut simplement regarder le présent (raisonnement par récurrence) et se l'approprier ....

:lol3:

[paquito]

j'ai appris en pensant et en appliquant correctement les règles de calcul ou des raisonnements (par récurrence par exemple)

supposons multiple de 3 pour n pair

alors

alors l'hypothèse de récurrence et la propriété " si a et b sont multiples de c alors a + b est multiple de c" permettent de conclure ...


et il est à noter qu'une lecture attentive de l'énoncé (mais on m'a aussi appris à lire ... correctement) impose la récurrence de 2 en 2 puisqu'on dit que n est pair ....

et c'est le pourquoi de mon premier post ... pour revenir à une récurrence "normale"

de toute façon donner une réponse complète n'est pas de l'instruction .... et laisse l'étudiant dans l'illusion de l'apprentissage ....


ensuite avant d'aller voir plus loin on peut simplement regarder le présent (raisonnement par récurrence) et se l'approprier ....

:lol3:

Le raisonnement par récurrence est une possibilité; l'usage des congruences constituait une alternative puisque c'est quand même un exercice d'arithmétique. Quand à savoir à quel moment il faut donner des informations plus complètes, tout dépend de l'élève; si visiblement il n'avance pas, comprendre une solution abrégée constitue en soi un exercice, sinon, je suis d'accord avec toi, si on peut se contenter de débloquer la situation, c'est plus satisfaisant. sans rancune :happy3:

[MATRIX02]

Je me permet de continuer avec ce que j'ai appris

1)

supposons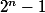 multiple de 3 pour n pair

Initialisation :
A(2) : est divisible par 3

Hérédité :
On suppose "A(n):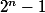 divisible par 3" vraie,
alors il existe k appartenant à N tels que

Récurrence :


k appartenant à N, A(n+2) est vraie, on a donc montré par récurrence
que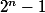 est divisible par 3 pour tout n appartenant à N


2)
Initialisation:
Je suppose que ;


on a , donc A(0) n'est pas divisible par 3

Héredité :

là je bloque -> en utilisant le 1) justifier que An est divisible par 3 ?

[beagle]

tu ne devrais pas commencer par n=0 parce que cela ne te donne pas une puissance paire,
tu vois que ton deuxième terme est 2^1
ce que tu as fait en 1) marchait avec des puissances paires.

commence avec n=1, si tu veux avoir une puissances paires, sic!

maintenant on te demande de justifier, pas forcément avec de la récurrence

(3k +1) + (3k'+1) + 1 devrait suffire.

[paquito]

Je me permet de continuer avec ce que j'ai appris

1)

supposons multiple de 3 pour n pair

Initialisation :
A(2) : est divisible par 3

Hérédité :
On suppose "A(n): divisible par 3" vraie,
alors il existe k appartenant à N tels que

Récurrence :


k appartenant à N, A(n+2) est vraie, on a donc montré par récurrence
que est divisible par 3 pour tout n appartenant à N


2)
Initialisation:
Je suppose que ;


on a , donc A(0) n'est pas divisible par 3

Héredité :

là je bloque -> en utilisant le 1) justifier que An est divisible par 3 ?

tu peux écrire , de même ; après, ça vient tout seul. Il n'y a pas de récurrence; tout découle de la question précédente.

[MATRIX02]

tu peux écrire , de même ; après, ça vient tout seul. Il n'y a pas de récurrence; tout découle de la question précédente.

1 ma première partie est-elle bonne ?

2 pourquoi je peux écrire ça !?, je suis un peu "largué" là

, de même

[beagle]

1 ma première partie est-elle bonne ?

2 pourquoi je peux écrire ça !?, je suis un peu "largué" là

, de même

Le 1) est pas mal.
Perso j'enlèverai la première phrase
supposons machin vrai,
avant l'initialisation.
puisque l'initialisation ne suppose rien, elle vérifie de visu,
m'enfin ça c'est de l'écriture.
Toujours dans le 1), n'oublie pas de mettre dans ta dernière phrase de conclusion:
pour tout n pair.

2)pour cette partie
ben si
a-1 est divisble par 3
a-1 = 3k
a = 3k+1

et le a c'est le truc que tu as démontré en 1), avec l'écriture de 2)
a savoir si 2^n est un nombre pair.
dans l'exo 2 nous ne sommes plus avec la retrictionn est pair , mais par contre 2^n doit ètre pair,
ce qui enlève le cas n=0 comme tu en as fait l'expérience dans ton essai d'intialisation qui ne marchait pas.

[paquito]

1 ma première partie est-elle bonne ?

2 pourquoi je peux écrire ça !?, je suis un peu "largué" là

, de même

1) Tu n'as pas fais l'initialisation pour qui est un nombre pair.

2) pour , est pair, donc d'après la question 1) est un multiple de , il existe donc un entier tel que
Même chose avec , sauf que tu prends puisque est utilisé avant.

[MATRIX02]

Ma version rédigée :

1)

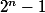multiple de 3 pour n pair

Initialisation :
est divisible par 3

Hérédité :
On suppose "A(n):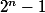 divisible par 3" vraie,
alors il existe k appartenant à N tels que

alors

Récurrence :


k appartenant à N, A(n+2) est vraie, on a donc montré par récurrence
que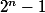 est divisible par 3 pour tout n appartenant à N


2)

;


pour , 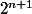est pair,

donc d'après la question 1) est un multiple de ,

il existe donc un entier tel que ,

il existe aussi un entier tel que

donc A(n) = (3k +1) + (3k'+1) + 1 est divisible par trois