juste une remarque ::
1/ ton énoncé initial parle de n non nul ....
2/ la récurrence de la question 1/ se fait sur les entiers pairs de N
Divisibilité par 3
24 messages
- Page 2 sur 2 - 1, 2
version corrigée :
1)
n est un entier naturel non nul et n est supposé être un nombre pair.
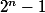 multiple de 3 pour n pair
multiple de 3 pour n pair
Initialisation :
: 2^2 - 1 = 3) est divisible par 3
est divisible par 3
Hérédité :
On suppose "A(n):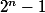 divisible par 3" vraie,
divisible par 3" vraie,
alors il existe k appartenant à N tels que
alors + 4 - 1 = 4(2^n - 1) + 3)
Récurrence :
 + 3 = 4(3k) +3 = 12k + 3)
k appartenant à N, A(n+2) est vraie, on a donc montré par récurrence
que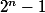 est divisible par 3 pour tout n appartenant à N
est divisible par 3 pour tout n appartenant à N
2)
=2^{2^{n+1}}+2^{2^n}+1) ;
;
pour ,
, 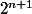 est pair,
est pair,
donc d'après la question 1) est un multiple de
est un multiple de  ,
,
il existe donc un entier tel que
tel que  ,
,
il existe aussi un entier tel que
tel que 
donc A(n) = (3k +1) + (3k'+1) + 1 est divisible par trois
1)
n est un entier naturel non nul et n est supposé être un nombre pair.
Initialisation :
Hérédité :
On suppose "A(n):
alors il existe k appartenant à N tels que
alors
Récurrence :
k appartenant à N, A(n+2) est vraie, on a donc montré par récurrence
que
2)
pour
donc d'après la question 1)
il existe donc un entier
il existe aussi un entier
donc A(n) = (3k +1) + (3k'+1) + 1 est divisible par trois
MATRIX02 a écrit:version corrigée :
1)
n est un entier naturel non nul et n est supposé être un nombre pair.multiple de 3 pour n pair
Initialisation :est divisible par 3
Hérédité :
On suppose "A(n):divisible par 3" vraie,
alors il existe k appartenant à N tels que
alors
Récurrence : + 3 = 4(3k) +3 = 12k + 3)
k appartenant à N, A(n+2) est vraie, on a donc montré par récurrence
queest divisible par 3 pour tout n appartenant à N
2);
pour,
est pair,
donc d'après la question 1)est un multiple de
,
il existe donc un entiertel que
,
il existe aussi un entiertel que
donc A(n) = (3k +1) + (3k'+1) + 1 est divisible par trois
c'est pas trop mal!!!
24 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 182 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
