Bonjour,
J'aimerai savoir si vous connaissiez la différence entre l'opération de modulo et de congruence ? Pour moi ça revient au même mis à part que la congruence peut prendre d'autres valeurs.
Par exemple 10 modulo 3 = 1 et et 10;) 1 [3] et ceci quelque soit les valeurs. En effet pour calculer la congruence et le modulo je fais la même opération:
Pour a;)b[n] et a mod n = b je fais: a - partie_entière(a/n)*n ce qui me donne la plus petite valeur de congruence. Sauf pour les négatifs ou je rajoute une fois n.
J'ai aussi fais plusieurs test sur des calculateurs en ligne et les valeurs sont les même
Modulo calculator :http://www.calculatorpro.com/calculator/modulo-calculator/
Congruence calculator (utiliser le 1er) : http://carrez.christophe.free.fr/spip.php?article128
Merci de m'éclairer sur ce sujet
Théo
Différence modulo et congruence ?
10 messages
- Page 1 sur 1
ttz a écrit:Bonjour,
J'aimerai savoir si vous connaissiez la différence entre l'opération de modulo et de congruence ? Pour moi ça revient au même mis à part que la congruence peut prendre d'autres valeurs.
Par exemple 10 modulo 3 = 1 et et 10;) 1 [3] et ceci quelque soit les valeurs. En effet pour calculer la congruence et le modulo je fais la même opération:
Pour a;)b[n] et a mod n = b je fais: a - partie_entière(a/n)*n ce qui me donne la plus petite valeur de congruence. Sauf pour les négatifs ou je rajoute une fois n.
J'ai aussi fais plusieurs test sur des calculateurs en ligne et les valeurs sont les même
Modulo calculator :http://www.calculatorpro.com/calculator/modulo-calculator/
Congruence calculator (utiliser le 1er) : http://carrez.christophe.free.fr/spip.php?article128
Merci de m'éclairer sur ce sujet
Théo
Salut !
On m'a toujours dis que c'était la même chose, cependant, je pense que tu dois confondre : tu veux sans doute parler de division euclidienne (cas particulier où le reste est compris entre 0 et n-1) ?
Par exemple 30 est congru à 14 modulo 16 mais aussi à -2 modulo 16.
Cependant le reste dans la division euclidienne de 30 par 16 est uniquement 14 :+++:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
capitaine nuggets a écrit:Salut !
On m'a toujours dis que c'était la même chose, cependant, je pense que tu dois confondre : tu veux sans doute parler de division euclidienne (cas particulier où le reste est compris entre 0 et n-1) ?
Par exemple 30 est congru à 14 modulo 16 mais aussi à -2 modulo 16.
Cependant le reste dans la division euclidienne de 30 par 16 est uniquement 14 :+++:
Oui c'est ça le reste de la division euclidienne. Au final ça revient au même si on cherche la plus petite valeur de congruence positive. Mais pour dire que deux nombres sont congruents c'est différent.
Merci
[quote="ttz"]Bonjour,
J'aimerai savoir si vous connaissiez la différence entre l'opération de modulo et de congruence ? Pour moi ça revient au même mis à part que la congruence peut prendre d'autres valeurs.
Par exemple 10 modulo 3 = 1 et et 10;) 1 [3] et ceci quelque soit les valeurs. En effet pour calculer la congruence et le modulo je fais la même opération:
Pour a;)b[n] et a mod n = b je fais: a - partie_entière(a/n)*n ce qui me donne la plus petite valeur de congruence. Sauf pour les négatifs ou je rajoute une fois n.
J'ai aussi fais plusieurs test sur des calculateurs en ligne et les valeurs sont les même
Modulo calculator :http://www.calculatorpro.com/calculator/modulo-calculator/
Congruence calculator (utiliser le 1er) : http://carrez.christophe.free.fr/spip.php?article128
Merci de m'éclairer sur ce sujet
ça ne marche qu'avec le même congruo!
J'aimerai savoir si vous connaissiez la différence entre l'opération de modulo et de congruence ? Pour moi ça revient au même mis à part que la congruence peut prendre d'autres valeurs.
Par exemple 10 modulo 3 = 1 et et 10;) 1 [3] et ceci quelque soit les valeurs. En effet pour calculer la congruence et le modulo je fais la même opération:
Pour a;)b[n] et a mod n = b je fais: a - partie_entière(a/n)*n ce qui me donne la plus petite valeur de congruence. Sauf pour les négatifs ou je rajoute une fois n.
J'ai aussi fais plusieurs test sur des calculateurs en ligne et les valeurs sont les même
Modulo calculator :http://www.calculatorpro.com/calculator/modulo-calculator/
Congruence calculator (utiliser le 1er) : http://carrez.christophe.free.fr/spip.php?article128
Merci de m'éclairer sur ce sujet
ça ne marche qu'avec le même congruo!
salut
il y a une différence fondamentale entre la congruence et "le modulo"
la (relation de) congruence est une relation entre deux nombres
les nombres a et b sont congrus ou non modulo un entier n
et cette relation permet de comparer tous les entiers ...
et l'ensemble des nombres x congrus à a modulo n est simplement l'ensemble des entiers qui ont même reste dans la division euclidienne par n ... (donc les nombres a + kn)
ainsi modulo 3 les nombres congrus à 10 sont tous les nombres 3k + 1
et dire 10 modulo 3 = 1 est un abus de langage qui consiste à donner un nombre qui a même reste que 10 dans la division euclidienne par 3
et je décide moi que 10 modulo 3 = 31
et alors on a la relation 10 congru à 1 congru à 31 (modulo 3)
il y a donc une très grande différence !!!!
il y a une différence fondamentale entre la congruence et "le modulo"
la (relation de) congruence est une relation entre deux nombres
les nombres a et b sont congrus ou non modulo un entier n
et cette relation permet de comparer tous les entiers ...
et l'ensemble des nombres x congrus à a modulo n est simplement l'ensemble des entiers qui ont même reste dans la division euclidienne par n ... (donc les nombres a + kn)
ainsi modulo 3 les nombres congrus à 10 sont tous les nombres 3k + 1
et dire 10 modulo 3 = 1 est un abus de langage qui consiste à donner un nombre qui a même reste que 10 dans la division euclidienne par 3
et je décide moi que 10 modulo 3 = 31
et alors on a la relation 10 congru à 1 congru à 31 (modulo 3)
il y a donc une très grande différence !!!!
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Bonjour,
sur toutes les calculettes il y a une touche "mod" qui effectue l'opération "reste de la division euclidienne"
comme on écrirait avec l'opération d'addition 10 + 3 = 13, c'est la même signification "syntactique"
et là on met bien le doigt sur la clé de ce faux problème
la relation de congruence est une relation (une relation d'équivalence même), au même titre que "=" ou " " ou "
" ou "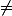 " etc etc
" etc etc
l'opération "mod" est une opération, qui comme toute opération donne un résultat à partir de deux données.
que le résultat de cette opération "mod" satisfasse à la relation "congruence" certes, on va dire que c'est fait pour (en fait c'est comme ça qu'est définie la relation de congruence)
a est congru à b modulo m :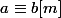 si et seulement si a mod m = b mod m
si et seulement si a mod m = b mod m
(si et seulement si le reste de la division euclidienne de a par m est le même que le reste de la division euclidienne de b par m)
mais si voyons.zygomatique a écrit:l'écriture 10 mod 3 = 1 ne veut rien dire !!
sur toutes les calculettes il y a une touche "mod" qui effectue l'opération "reste de la division euclidienne"
comme on écrirait avec l'opération d'addition 10 + 3 = 13, c'est la même signification "syntactique"
et là on met bien le doigt sur la clé de ce faux problème
la relation de congruence est une relation (une relation d'équivalence même), au même titre que "=" ou "
l'opération "mod" est une opération, qui comme toute opération donne un résultat à partir de deux données.
que le résultat de cette opération "mod" satisfasse à la relation "congruence" certes, on va dire que c'est fait pour (en fait c'est comme ça qu'est définie la relation de congruence)
a est congru à b modulo m :
(si et seulement si le reste de la division euclidienne de a par m est le même que le reste de la division euclidienne de b par m)
mathafou a écrit:Bonjour,mais si voyons.
sur toutes les calculettes il y a une touche "mod" qui effectue l'opération "reste de la division euclidienne"
comme on écrirait avec l'opération d'addition 10 + 3 = 13, c'est la même signification "syntactique"
et là on met bien le doigt sur la clé de ce faux problème
la relation de congruence est une relation (une relation d'équivalence même), au même titre que "=" ou "" ou "
" etc etc
l'opération "mod" est une opération, qui comme toute opération donne un résultat à partir de deux données.
que le résultat de cette opération "mod" satisfasse à la relation "congruence" certes, on va dire que c'est fait pour (en fait c'est comme ça qu'est définie la relation de congruence)
a est congru à b modulo m :si et seulement si a mod m = b mod m
(si et seulement si le reste de la division euclidienne de a par m est le même que le reste de la division euclidienne de b par m)
c'est exactement ce que je disais dans mon premier post ...
:lol3:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Il est primordial de ne pas confondre la relation de congruence avec la division euclidienne;
on a

 , ce qui rend la relation de récurrence compatible avec + et x .
, ce qui rend la relation de récurrence compatible avec + et x .
Ce qui permet beaucoup de choses:
exemple:
10^0=1[7]
10^1=3[7], donc 10^2=3x3=9=2[7]; 10^3=2x3=6=-1[7]; puis 10^4=-3[7] et 10^5=-9=-2[7] et enfin 10^6=-6=1[7] et un nouveau cycle recommence.
On a aussi 2999997=3x10^6-3x10^0=1-1=0[7];
les congruences permettent de faire beaucoup de choses; on peut même multiplier des congruences de modulos différents à conditions de multiplier les modulos;
on a
Ce qui permet beaucoup de choses:
exemple:
10^0=1[7]
10^1=3[7], donc 10^2=3x3=9=2[7]; 10^3=2x3=6=-1[7]; puis 10^4=-3[7] et 10^5=-9=-2[7] et enfin 10^6=-6=1[7] et un nouveau cycle recommence.
On a aussi 2999997=3x10^6-3x10^0=1-1=0[7];
les congruences permettent de faire beaucoup de choses; on peut même multiplier des congruences de modulos différents à conditions de multiplier les modulos;
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 80 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
