La congruence modulo n

[zaira]

Bonjour à toutes et tous
je suis bloquée dans une petite question ,est ce que vous pouvez m'aider?
la question est :
montrer que 2^n ≡1 modulo(9) ⇒ 2^n ≡1modulo (7)

Et merci !!

[aviateur]

Bonjour
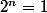
(1) Le plus petit n (autre que n=0) tel que mod 9 est n=6 (c'est vite vérifié).

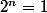
(2) Alors on a mod 9 ssi n est un multiple de 6.

(3) Mais 2^6=1 mod 7 (théorème de Fermat mais c'est aussi facile à vérifier)
(4) implique que si n est multiple de 6 alors 2^n=1 mod 7 .CQFD

[zaira]

j'ai pas compris la méthode avec laquelle vous avez raisonné

[aviateur]

J'ai mis un numéro à chaque ligne:
quelle ligne n'as tu pas compris?

[zaira]

la 3 ème ligne je n'ai pas étudié le théorème de farmat c à d que je ne sais pas son principe

[Lostounet]

Bonjour à toutes et tous
je suis bloquée dans une petite question ,est ce que vous pouvez m'aider?
la question est :
montrer que 2^n ≡1 modulo(9) ⇒ 2^n ≡1modulo (7)

Et merci !!

Salut,
Ce qu'Aviateur te propose c'est de résoudre la première équation 2^n=1 mod 9

Avec un petit tableau, tu trouves que c'est n=6 (mod 9) donc n est de la forme n=9k+6 avec k un entier.

Ensuite tu vérifies que n=9k + 6 satisfait à:
2^n = 1 mod 7.

2^(9k+6)= 2^(9k) * 2^6
= (2^3)^(3k)*(2^3)^2
= 1^(3k) * 1^2 (mod 7) puisque 2^3=8=1 mod 7.

Tu n'as pas vraiment besoin du théorème de Fermat (mais ça fait plus joli si tu le connais).

[zaira]

merci beaucoup j'ai compris
mais pouvez-vous me dire de quel tableau vous parlez?

[Lostounet]

Comment tu résous 2^n = 1 mod 9 ?


Tu fais:
n=1 mod 9 implique 2^n=2 mod 9
n=2 mod 9 implique 2^n= 4 mod 9
Etc...
Jusqu'à trouver un certain n pour que 2^n=1 (mod 9)

C'est un tableau de valeurs.

[zaira]

ahhh oui j'ai oubli
merci beaucoup