Devoir sur les vecteurs (seconde )
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
cinthyasnape
- Membre Naturel
- Messages: 39
- Enregistré le: 15 Sep 2014, 11:52
-
 par cinthyasnape » 15 Sep 2014, 11:57
par cinthyasnape » 15 Sep 2014, 11:57
Bonjour a tous j'ai un DM de Math sur les vecteur a faire si quelquun pourrez m'aider ça serrais sympa :) je n'y arriive pas trop
ABCD est un triangle (non aplati) G est le point du plan tel que : GA+GB+GC=0.Il est le milieu de [bc]
1 démontrer que BG-CA°CB-AG=O
2 démontrer que BI+CB-GI=CG
3 Démontrer que GA=2GI.Que peut on en déduire?
4 M est un point quelconque du plan.Démontrer que 3MG=MA+MB+MC
merci d'avance :)
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 15 Sep 2014, 12:03
par Shew » 15 Sep 2014, 12:03
cinthyasnape a écrit:Bonjour a tous j'ai un DM de Math sur les vecteur a faire si quelquun pourrez m'aider ça serrais sympa

je n'y arriive pas trop
ABCD est un triangle (non aplati) G est le point du plan tel que : GA+GB+GC=0.Il est le milieu de [bc]
1 démontrer que BG-CA°CB-AG=O
2 démontrer que BI+CB-GI=CG
3 Démontrer que GA=2GI.Que peut on en déduire?
4 M est un point quelconque du plan.Démontrer que 3MG=MA+MB+MC
merci d'avance

Pas compris celle-ci : 1 démontrer que BG-CA°CB-AG=O
Le degrés que represente t'il ?
-
cinthyasnape
- Membre Naturel
- Messages: 39
- Enregistré le: 15 Sep 2014, 11:52
-
 par cinthyasnape » 15 Sep 2014, 13:08
par cinthyasnape » 15 Sep 2014, 13:08
Shew a écrit:Pas compris celle-ci : 1 démontrer que BG-CA°CB-AG=O
Le degrés que represente t'il ?
excuser moi ça veut dire + c'est BG-CA+AG=O
mais sur les lettre BG,CA et AG il y a des flèche au dessus vu que c'est des vecteur
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 15 Sep 2014, 14:16
par Shew » 15 Sep 2014, 14:16
cinthyasnape a écrit:excuser moi ça veut dire + c'est BG-CA+AG=O
mais sur les lettre BG,CA et AG il y a des flèche au dessus vu que c'est des vecteur
On peut appliquer la chose ainsi
 - \vec{AG})
. Appliquez la relation de Chasles et faites disparaître le signe négatif devant les vecteurs concernés .
-
cinthyasnape
- Membre Naturel
- Messages: 39
- Enregistré le: 15 Sep 2014, 11:52
-
 par cinthyasnape » 15 Sep 2014, 14:39
par cinthyasnape » 15 Sep 2014, 14:39
Shew a écrit:On peut appliquer la chose ainsi
 - \vec{AG})
. Appliquez la relation de Chasles et faites disparaître le signe négatif devant les vecteurs concernés .
Je connais la relation de Chasles mais je n'y arrive pas
-
cinthyasnape
- Membre Naturel
- Messages: 39
- Enregistré le: 15 Sep 2014, 11:52
-
 par cinthyasnape » 15 Sep 2014, 14:40
par cinthyasnape » 15 Sep 2014, 14:40
Shew a écrit:On peut appliquer la chose ainsi
 - \vec{AG})
. Appliquez la relation de Chasles et faites disparaître le signe négatif devant les vecteurs concernés .
merci de ta réponse

-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 15 Sep 2014, 15:14
par Shew » 15 Sep 2014, 15:14
cinthyasnape a écrit:Je connais la relation de Chasles mais je n'y arrive pas
Regardez bien on a

, on veut que le signe de négation disparaisse donc on a :
 + \vec{CB} = \vec{AC} + \vec{CB})
. Maintenant en utilisant Chasles vous pouvez ajouter

et
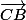
entre eux .
-
cinthyasnape
- Membre Naturel
- Messages: 39
- Enregistré le: 15 Sep 2014, 11:52
-
 par cinthyasnape » 15 Sep 2014, 19:14
par cinthyasnape » 15 Sep 2014, 19:14
Shew a écrit:Regardez bien on a

, on veut que le signe de négation disparaisse donc on a :
 + \vec{CB} = \vec{AC} + \vec{CB})
. Maintenant en utilisant Chasles vous pouvez ajouter

et
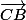
entre eux .
Oui d'accord merci je crois que j'ai comprit

ça fait :
BG+(-CA+CB)-AC
=-( -CA+CB)
=AC+CB
=AC=0
c'est ça non ?
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 15 Sep 2014, 19:17
par Shew » 15 Sep 2014, 19:17
cinthyasnape a écrit:Oui d'accord merci je crois que j'ai comprit

ça fait :
BG+(-CA+CB)-AC
=-( -CA+CB)
=AC+CB
=AC=0
c'est ça non ?
Non on verra
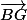
et
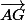
après, en utilisant la relation de Chasles calculez

-
cinthyasnape
- Membre Naturel
- Messages: 39
- Enregistré le: 15 Sep 2014, 11:52
-
 par cinthyasnape » 15 Sep 2014, 20:40
par cinthyasnape » 15 Sep 2014, 20:40
Shew a écrit:Non on verra
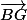
et
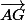
après, en utilisant la relation de Chasles calculez

Mais je comprend pas comment je peut le calculer puisque je n'ai pas de chiffre qui les représente
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 15 Sep 2014, 20:42
par Shew » 15 Sep 2014, 20:42
cinthyasnape a écrit:Mais je comprend pas comment je peut le calculer puisque je n'ai pas de chiffre qui les représente
:hein: :hein: :hein: Vous avez bien appris la relation de Chasles ?
-
cinthyasnape
- Membre Naturel
- Messages: 39
- Enregistré le: 15 Sep 2014, 11:52
-
 par cinthyasnape » 15 Sep 2014, 20:51
par cinthyasnape » 15 Sep 2014, 20:51
Shew a écrit::hein: :hein: :hein: Vous avez bien appris la relation de Chasles ?
Oui pour définition on as de marquer
AB+BC=AC
Du coup AC+CB=AB?
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 15 Sep 2014, 21:16
par Shew » 15 Sep 2014, 21:16
cinthyasnape a écrit:Oui pour définition on as de marquer
AB+BC=AC
Du coup AC+CB=AB?
Voila c'est bon . Maintenant on se concentre sur

transformez ce vecteur de façon à ce que son signe soit positif .
-
cinthyasnape
- Membre Naturel
- Messages: 39
- Enregistré le: 15 Sep 2014, 11:52
-
 par cinthyasnape » 15 Sep 2014, 21:39
par cinthyasnape » 15 Sep 2014, 21:39
Shew a écrit::hein: :hein: :hein: Vous avez bien appris la relation de Chasles ?
D'accord alors...
-(-AG)+BG=AG+BG
c'est correcte ?
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 15 Sep 2014, 21:43
par Shew » 15 Sep 2014, 21:43
cinthyasnape a écrit:D'accord alors...
-(-AG)+BG=AG+BG
c'est correcte ?
On se concentre sur
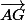
uniquement ne soyez donc pas pressé . Non le changement n'est pas correct il ne suffit pas de mettre moins devant pour faire disparaître la negation, il faut appliquer un changement directement sur le vecteur
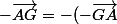 = \vec{GA})
Maintenant utilisez Chasles pour trouver la somme de

-
cinthyasnape
- Membre Naturel
- Messages: 39
- Enregistré le: 15 Sep 2014, 11:52
-
 par cinthyasnape » 15 Sep 2014, 21:52
par cinthyasnape » 15 Sep 2014, 21:52
Shew a écrit:On se concentre sur
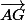
uniquement ne soyez donc pas pressé . Non le changement n'est pas correct il ne suffit pas de mettre moins devant pour faire disparaître la negation, il faut appliquer un changement directement sur le vecteur
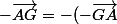 = \vec{GA})
Maintenant utilisez Chasles pour trouver la somme de

Ha oui merci je viens de comprendre la transformation -AG est le vecteur opposé de GA
pour trouvé la somme de GA+AB
On utilise Chasles
qui dit que
AB+BC=AC
donc GA+AB=GB ?
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 16 Sep 2014, 05:01
par Shew » 16 Sep 2014, 05:01
cinthyasnape a écrit:Ha oui merci je viens de comprendre la transformation -AG est le vecteur opposé de GA
pour trouvé la somme de GA+AB
On utilise Chasles
qui dit que
AB+BC=AC
donc GA+AB=GB ?
C'est ca et maintenant que vous avez compris le concept des opposés calculez

-
cinthyasnape
- Membre Naturel
- Messages: 39
- Enregistré le: 15 Sep 2014, 11:52
-
 par cinthyasnape » 16 Sep 2014, 19:43
par cinthyasnape » 16 Sep 2014, 19:43
Shew a écrit:C'est ca et maintenant que vous avez compris le concept des opposés calculez

C'est égale a BB non ?
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 16 Sep 2014, 19:47
par Shew » 16 Sep 2014, 19:47
cinthyasnape a écrit:C'est égale a BB non ?
Et
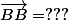
-
cinthyasnape
- Membre Naturel
- Messages: 39
- Enregistré le: 15 Sep 2014, 11:52
-
 par cinthyasnape » 16 Sep 2014, 20:06
par cinthyasnape » 16 Sep 2014, 20:06
Shew a écrit:Et
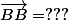
Heu je ne sais pas trop j'aurais dit GG mais je pense que c'est faux
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 103 invités
je n'y arriive pas trop
uniquement ne soyez donc pas pressé . Non le changement n'est pas correct il ne suffit pas de mettre moins devant pour faire disparaître la negation, il faut appliquer un changement directement sur le vecteur
Maintenant utilisez Chasles pour trouver la somme de
