Devoir sur les vecteurs (seconde )
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 16 Sep 2014, 20:08
par Shew » 16 Sep 2014, 20:08
cinthyasnape a écrit:Heu je ne sais pas trop j'aurais dit GG mais je pense que c'est faux
Alors laissez tombé

et donnez moi plutot le vecteur opposé de
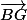
.
-
cinthyasnape
- Membre Naturel
- Messages: 39
- Enregistré le: 15 Sep 2014, 11:52
-
 par cinthyasnape » 16 Sep 2014, 20:30
par cinthyasnape » 16 Sep 2014, 20:30
Shew a écrit:Alors laissez tombé

et donnez moi plutot le vecteur opposé de
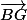
.
le vecteur opposé de BG est GB
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 16 Sep 2014, 20:35
par Shew » 16 Sep 2014, 20:35
cinthyasnape a écrit:le vecteur opposé de BG est GB
Non, on a déja vu ca plus haut .
-
cinthyasnape
- Membre Naturel
- Messages: 39
- Enregistré le: 15 Sep 2014, 11:52
-
 par cinthyasnape » 16 Sep 2014, 20:42
par cinthyasnape » 16 Sep 2014, 20:42
Shew a écrit:Non, on a déja vu ca plus haut .
ce n'est pas -GB?
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 16 Sep 2014, 20:43
par Shew » 16 Sep 2014, 20:43
cinthyasnape a écrit:ce n'est pas -GB?
Voillaa donc que vaut

?
-
cinthyasnape
- Membre Naturel
- Messages: 39
- Enregistré le: 15 Sep 2014, 11:52
-
 par cinthyasnape » 16 Sep 2014, 21:02
par cinthyasnape » 16 Sep 2014, 21:02
Shew a écrit:Voillaa donc que vaut

?
BG+GB vaut BB
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 16 Sep 2014, 21:11
par Shew » 16 Sep 2014, 21:11
cinthyasnape a écrit:BG+GB vaut BB
Pourquoi revenir la dessus puisque vous me disiez plus haut que le vecteur opposé de
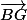
etait

?
-
cinthyasnape
- Membre Naturel
- Messages: 39
- Enregistré le: 15 Sep 2014, 11:52
-
 par cinthyasnape » 16 Sep 2014, 21:16
par cinthyasnape » 16 Sep 2014, 21:16
Shew a écrit:Pourquoi revenir la dessus puisque vous me disiez plus haut que le vecteur opposé de
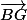
etait

?
je sais pas je me pers un peut...
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 16 Sep 2014, 21:20
par Shew » 16 Sep 2014, 21:20
cinthyasnape a écrit:je sais pas je me pers un peut...
Donc
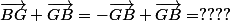
-
cinthyasnape
- Membre Naturel
- Messages: 39
- Enregistré le: 15 Sep 2014, 11:52
-
 par cinthyasnape » 17 Sep 2014, 13:43
par cinthyasnape » 17 Sep 2014, 13:43
Shew a écrit:Donc
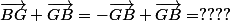
c'est égale vecteur nul 0
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 17 Sep 2014, 13:50
par Shew » 17 Sep 2014, 13:50
cinthyasnape a écrit:c'est égale vecteur nul 0
Voila CQFD
-
cinthyasnape
- Membre Naturel
- Messages: 39
- Enregistré le: 15 Sep 2014, 11:52
-
 par cinthyasnape » 17 Sep 2014, 17:59
par cinthyasnape » 17 Sep 2014, 17:59
Shew a écrit:Voila CQFD
c'est quoi ? j'ai pas comprit ?
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 17 Sep 2014, 18:01
par Shew » 17 Sep 2014, 18:01
cinthyasnape a écrit:c'est quoi ? j'ai pas comprit ?
Pour faire court, c'est bon :lol3:
-
cinthyasnape
- Membre Naturel
- Messages: 39
- Enregistré le: 15 Sep 2014, 11:52
-
 par cinthyasnape » 17 Sep 2014, 18:04
par cinthyasnape » 17 Sep 2014, 18:04
Shew a écrit:Pour faire court, c'est bon :lol3:
Ha ! d'accord merci

-
cinthyasnape
- Membre Naturel
- Messages: 39
- Enregistré le: 15 Sep 2014, 11:52
-
 par cinthyasnape » 17 Sep 2014, 18:05
par cinthyasnape » 17 Sep 2014, 18:05
cinthyasnape a écrit:Ha ! d'accord merci

Du coup la question 1 est fini

on peut passer a la question 2

-
Moicoucou
- Membre Relatif
- Messages: 138
- Enregistré le: 11 Aoû 2014, 00:14
-
 par Moicoucou » 17 Sep 2014, 18:06
par Moicoucou » 17 Sep 2014, 18:06
CQFD = Ce Qu'il Fallait Démontrer
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 17 Sep 2014, 18:14
par Shew » 17 Sep 2014, 18:14
cinthyasnape a écrit:Du coup la question 1 est fini

on peut passer a la question 2

A l'aide de Chasles transformez le vecteur
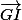
en fonction de
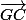
-
cinthyasnape
- Membre Naturel
- Messages: 39
- Enregistré le: 15 Sep 2014, 11:52
-
 par cinthyasnape » 19 Sep 2014, 19:16
par cinthyasnape » 19 Sep 2014, 19:16
Shew a écrit:A l'aide de Chasles transformez le vecteur
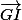
en fonction de
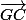
Excusez moi mais je ne comprend pas...
je sais que Chaskes dit que AB+BC=AC
Et qu'il faut que je démontre BI+CB-GI=CG,
mais c'est a dire transformé GI en fonction de GC ?
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 19 Sep 2014, 22:22
par Shew » 19 Sep 2014, 22:22
cinthyasnape a écrit:Excusez moi mais je ne comprend pas...
je sais que Chaskes dit que AB+BC=AC
Et qu'il faut que je démontre BI+CB-GI=CG,
mais c'est a dire transformé GI en fonction de GC ?
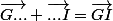
Petite erreur de ma part plus haut concernant la définition du vecteur opposé, le vecteur opposé de
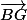
est bien
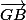
mais dans ce cas je voulais dire "
exprimer le vecteur 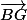 en fonction de son vecteur opposé
en fonction de son vecteur opposé" . Donc on a
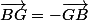
-
cinthyasnape
- Membre Naturel
- Messages: 39
- Enregistré le: 15 Sep 2014, 11:52
-
 par cinthyasnape » 20 Sep 2014, 12:32
par cinthyasnape » 20 Sep 2014, 12:32
Shew a écrit: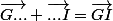
Petite erreur de ma part plus haut concernant la définition du vecteur opposé, le vecteur opposé de
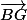
est bien
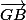
mais dans ce cas je voulais dire "
exprimer le vecteur 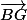 en fonction de son vecteur opposé
en fonction de son vecteur opposé" . Donc on a
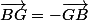
Donc pour résumer la question 1,on a fait ceci
BG + (-CA +CB)-AG
-AC+CB=AC+CB
AC+CB=AB
-AG=-(GA)=GA
GA+AB=GB
BG+GB=-GB+GB=0
pour la question 2
démontrer que BI+CB-GI=CG
vous me dites de "transformez le vecteur GI en fonction de GC"
oui CI...+..i=GI,heu..j'ai toujours pas compris
mon professeur de math m'a dit "d'insérer le point G (en utilisant Chasles) dans chacun des vecteurs de gauche et la simplification s'opère tout de suite pour trouver le vecteur CG" mais j'ai pas comprit Je ne comprend vraiment rien....
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 62 invités
est bien
mais dans ce cas je voulais dire "exprimer le vecteur
en fonction de son vecteur opposé" . Donc on a