Devoir de mathematiques Terminale

[arture]

Bonjour a tous,
Alors voila j'ai un devoir de mathématiques et je n'arrive pas a le finir.

On considère la fonction f définie sur ]-2;+infini[ par f(x)=ax+b+(c/(x-d)). a,b,c et d étant des nombres réels que l'on déterminera en répondant aux questions du problème.

Soit f'(x) la fonction dérivée de la fonction f sur ]-2;+infini[
On note C et C' les courbes représentant respectivement f et f' dans le repère (o;i,j)
La droite D ayant pour équation x=-2, est asymptote aux courbes C et C'. La droite delta, ayant pour équation y=2, est asymptote à la courbe C'.
C passe par le point de coordonnées (-1;-1) et admet en ce point une tangente parallèle à l'axe des abscisses.


1) Quelles hypothèses de l'énoncé permettent de justifier que d=-2 ?
2) Exprimer f'(x) à l'aide des nombre a,b et c.
3) Justifier que lim f'(x) quand x tend vers +infini = a. En déduire la valeur de a
4) Calculer c en utilisant f'(-1).
5) Calculer b en utilisant f(-1).
6) Vérifier que lim (f(x)-(2x-1)) quand x tend vers +infini =0
7) La courbe C admet-elle une tangente parallèle à la droite d'équation y=2x-1 ? Justifier."


Voila le sujet j'ai déjà fait les 2 premières questions mais je bloque pourriez vous m'aider a faire la question 3 et je pense qu'après je pourrais me débrouiller seul.



Merci a vous ,

[Anonyme]

3) Justifier que lim f'(x) quand x tend vers +infini = a. En déduire la valeur de a

Que veut dire (d'après la définition d'une asymptote horizontale à une courbe)

La droite delta, ayant pour équation y=2, est asymptote à la courbe C'

Conseil :
Il faut faire des dessins pour essayer de visualiser la forme de ces "courbes"

[arture]

Que veut dire (d'après la définition d'une asymptote horizontale à une courbe)

La droite delta, ayant pour équation y=2, est asymptote à la courbe C'

Conseil :
Il faut faire des dessins pour essayer de visualiser la forme de ces "courbes"

Ptinoir j'ai déjà les courbes représenter

[arture]

Pourrais t'on juste me donner la solution de la question 3 parce que cette leçon nous l'avons commencer y'a même pas 2 semaines et on avait jamais fait un exercice de ce type auparavant alors j'ai vraiment besoin d'aide ce dm est a rendre pour demain

[Anonyme]

@arture

Connais tu ce que veut dire

au niveau de la limite de la fonction quand tend vers

la phrase suivante ? :

La droite delta, ayant pour équation y=2, est asymptote à la courbe C'


ps)
je pense qu'il faut ajouter dans l'énoncé que cette droite asymptote à C' est au voisinage de +infini

[arture]

@arture

Connais tu ce que veut dire

au niveau de la limite de la fonction quand tend vers

la phrase suivante ? :

La droite delta, ayant pour équation y=2, est asymptote à la courbe C'


ps)
je pense qu'il faut ajouter dans l'énoncé que cette droite asymptote à C' est au voisinage de +infini

ptitnoir je comprend pas la phrase

[Anonyme]

Quelle est la définition d'une droite horizontale asymptote à une courbe en +infini ?

[arture]

Quelle est la définition d'une droite horizontale asymptote à une courbe en +infini ?

c'est une droite dont la courbe s'approche de l'infini mais sans jamais l'atteindre si je me souviens

[Anonyme]

c'est une droite dont la courbe s'approche de l'infini mais sans jamais l'atteindre si je me souviens

Je pense que tu voulais expliquer que :

la courbe se trouve "piégée dans un tuyau cylindrique centré autour de cette droite" quand x tend vers +infini

ET ce tuyau a un rayon de plus en plus petit
quand x tend vers +infini

Relis ton cours si besoin pour bien comprendre ce que je viens d'écrire ( en maths , il faut essayer d'être précis au niveau des explications )

Maintenant : Il y a une autre réponse ( ou explication ) qui concerne
la limite de cette fonction quand x tend vers +infini

Relis ton cours car c'est surement écrit quelque part....

[arture]

j'ai beau relire mon cours je comprend pas la question vous pourriez pas me donner une piste svp

[Anonyme]

@arture

Pour t'aider à comprendre

1)
Peux tu tracer sur ta calculatrice la fonction f définie par

2)
Regarde en et que constates tu ?

3)
Est ce que la droite d'équation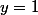 est une asymptote à la courbe au voisinage de ?

4)
Est ce que tu comprends que :


Si tu as compris : applique le même raisonnement à ta fonction de ton exercice

[arture]

@arture

Pour t'aider à comprendre

1)
Peux tu tracer sur ta calculatrice la fonction f définie par

2)
Regarde en et que constates tu ?

3)
Est ce que la droite d'équation est une asymptote à la courbe au voisinage de ?

4)
Est ce que tu comprends que :


Si tu as compris : applique le même raisonnement à ta fonction de ton exercice

tu te serai pas tromper c'est pas -1 au du de 1?

[Anonyme]

tu te serai pas tromper c'est pas -1 au du de 1?

OUI Bravo donc je pense que tu as compris

[arture]

OUI Bravo donc je pense que tu as compris

Je pense donc la valeur de a est 2 f'(x)=2 quand x tend vers + infini
4) C=6 c'est juste ?

[Anonyme]

@arture
Désolé je n'ai pas fait les calculs

Tout ce que je peux écrire c'est que la fonction f définie par f(x)=ax+b+(c/(x-d))
est dérivable sur son domaine de définition ( qui est IR \ { d} )

et on a : si x est différent de d

f'(x)=a-c/(x-d)^2

[math-69]

bonjour, je suis coincer a la 3ème ques. je ne comprend pas la démarche à suivre. pouriez vous m'aider svp