" on divise un polynôme p(x) par x-1 le reste est 6
on divise un polynôme p(x) par x-2 le reste est 8
quel est le reste de la division euclidienne de p(x) avec (x-1)(x-2) "
Bonjour, mon professeur de math m'a donné cette exercice et a dit qu'il mettra quelque chose comme ça dans le prochain devoir, donc j'ai vraiment besoin d'aide avant samedi.
s'il vous plait!!!!
Déterminer reste d'une division euclidienne
8 messages
- Page 1 sur 1
Re: déterminer reste d'une division euclidienne
Bonsoir,
commence à écrire l'égalité entre polynômes qui exprime la division du polynôme p par (x-1)(x-2).
On note Q son quotient et le R son reste.
commence à écrire l'égalité entre polynômes qui exprime la division du polynôme p par (x-1)(x-2).
On note Q son quotient et le R son reste.
Re: déterminer reste d'une division euclidienne
Bonjour,
Il me semble qu'il y a une arnaque là dessous.
Le reste de la division par (x-1)(x-2) ne peut pas être un nombre constant.
Exemple : soit P(x) = x³+x²-8x + 12
Le reste de la division de P(x)par (x-1) est 6, on a P(x) = (x²+2x-6)*(x-1) + 6
Le reste de la division de P(x)par (x-2) est 8, on a P(x) = (x²+3x-2)*(x-2) + 8
Mais si on divise P(x) par (x-1)(x-2), on arrive à P(x) = (x+4)(x-1)(x-2) + (2x+4)
Le reste (si on peut l'appeler ainsi) est ici 2x + 4 et donc pas une constante.
Me trompé-je ?

Il me semble qu'il y a une arnaque là dessous.
Le reste de la division par (x-1)(x-2) ne peut pas être un nombre constant.
Exemple : soit P(x) = x³+x²-8x + 12
Le reste de la division de P(x)par (x-1) est 6, on a P(x) = (x²+2x-6)*(x-1) + 6
Le reste de la division de P(x)par (x-2) est 8, on a P(x) = (x²+3x-2)*(x-2) + 8
Mais si on divise P(x) par (x-1)(x-2), on arrive à P(x) = (x+4)(x-1)(x-2) + (2x+4)
Le reste (si on peut l'appeler ainsi) est ici 2x + 4 et donc pas une constante.
Me trompé-je ?
Re: déterminer reste d'une division euclidienne
Bonjour
Et penser que le degré du reste est strictement inférieur à celui du diviseur...
Et penser que le degré du reste est strictement inférieur à celui du diviseur...
Re: déterminer reste d'une division euclidienne
Oui Blackjack le reste est un polynôme de degré 1...
Les hypothèses donnent un système qui fournit les coeff de ce reste.
Les hypothèses donnent un système qui fournit les coeff de ce reste.
Re: déterminer reste d'une division euclidienne
catamat a écrit:Oui Blackjack le reste est un polynôme de degré 1...
Les hypothèses donnent un système qui fournit les coeff de ce reste.
oui.
On divise le polynôme P par
Il existe deux polynômes Q et R tels que:
avec deg(R) < 2
Il existe donc deux réels a et b tels que
d'où
on a ensuite:
avec deg(a+b) < 1
l'égalité (*) est donc la division de P par (x-1)
a+b est le reste de la division de P par (x-1)
On en tire : a+b=6
De même:
l'égalité (**) est la division de P par (x-2)
2a+b est le reste de la division de P par (x-2)
d'où
2a+b=8
on a donc le système
d'où le calcul de a et b.
a=2 et b=4.
Re: déterminer reste d'une division euclidienne
Oui Mathelot je trouvais pareil mais P(1)=6 et P(2)=8 se déduisent immédiatement des hypothèses...
p(x)=(x-1)q(x)+6 donc p(1)=6 idem pour p(2)
on divise un polynôme p(x) par x-1 le reste est 6
on divise un polynôme p(x) par x-2 le reste est 8
p(x)=(x-1)q(x)+6 donc p(1)=6 idem pour p(2)
Re: déterminer reste d'une division euclidienne
Méthode proposée par la majorité
Le reste de la division de P par (x-1) est 6
Il existe un polynôme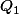 tel que
tel que
=(x-1)Q_1(x)+6)
D'où=6)
Le reste de la division de P par (x-2) est 8
Il existe un polynôme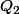 tel que
tel que
=(x-2)Q_2(x)+8)
D'où=8)
Divisons P par (x-1)(x-2)
Il existe deux polynômes Q et R tels que
=(x-1)(x-2)Q(x)+R(x))
le degré de R est strictement plus petit que 2
Il existe donc deux réels a et b tels que
=ax+b)
d'où
=(x-1)(x-2)Q(x)+ax+b)
Comme=6)
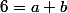
Comme P(2)=8
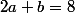
d'où+a=6+a=8)
d'où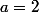
puis
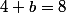
d'où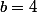
le reste R(x) est donc le polynôme=2x+4)
Le reste de la division de P par (x-1) est 6
Il existe un polynôme
D'où
Le reste de la division de P par (x-2) est 8
Il existe un polynôme
D'où
Divisons P par (x-1)(x-2)
Il existe deux polynômes Q et R tels que
le degré de R est strictement plus petit que 2
Il existe donc deux réels a et b tels que
d'où
Comme
Comme P(2)=8
d'où
d'où
puis
d'où
le reste R(x) est donc le polynôme
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 41 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
