Dérivée seconde d'une fonction

[scaly]

Bonjour,

Je suis bloqué sur la dérivée seconde d'une fonction qui est : y=
Ma dérivée première est : 3x.(x-2) / 2

Par contre pour la dérivée seconde, je me retrouve avec une équation sacrément longue et lorsque j'essaie de la simplifier, je ne tombe jamais sur quelque chose de cohérent.

Est-ce que quelqu'un saurait m'aider, et aurait une technique efficace pour ce genre de problème ?

Merci d'avance,

Alex

Ps : Existe-t-il un moyen d'écrire des formules mathématiques dans un message (pour la racine par exemple) ?

[Sa Majesté]

Ps : Existe-t-il un moyen d'écrire des formules mathématiques dans un message (pour la racine par exemple) ?

Salut

Oui, voir le dernier lien de ma signature
Pour la racine carrée c'est [tex ]\sqrt{x^2(x-3)}[/tex ], sans les espaces après tex :

[Sa Majesté]

Quel est le domaine de définition de la fonction ?

[scaly]

d'où dom f : 3 à + l'infini

Merci pour l'astuce Latex !

[Sa Majesté]

d'où dom f : 3 à + l'infini

Pas tout à fait
Il y a une subtilité car aussi pour x=0
Autrement dit le domaine de f est
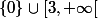
Ça ne change rien car 0 est un point isolé du domaine de définition de f donc on ne peut pas étudier la dérivabilité de f en 0
Considérons uniquement le cas où x est plus grand que 3
Ne peux-tu pas simplifier alors l'expression de f ?

[scaly]

En m'intéressant uniquement à ?

[Sa Majesté]

Oui
Tu peux simplifier

[Ericovitchi]

En te débrouillant bien tu dois tomber sur
f"(x)=

[scaly]

Simplifier en ?

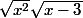
Je vais essayer...
Ce qui m'embête c'est lorsque je dérive, vaut-il mieux factoriser ou pas ?
Car lorsque je fais ma dérivée seconde, je me retrouve avec un numérateur très long et assez lourd à digérer pour la suite...

Edit : J'ai trouvé !

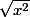
J'ai donc simplifié en x et c'est tout de suite plus léger.

Je trouve comme dérivée seconde :

Merci pour l'aide, ça faisait un moment que je tournais autour !

[Ericovitchi]

Attention, ça n'est pas celle que je t'ai donnée ! Et si je l'ai mise, c'est que je suis sûr. Donc prend tes responsabilités, mais la probabilité pour que ça soit toi qui ait raison est assez faible à mon avis.

[scaly]

Est-ce que vous pouvez m'expliquer brièvement comment vous en arrivez là alors car c'est justement ça qui me pose problème?

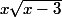
Et est-ce que dériver revient bien à la même chose ?

Merci.

[Ericovitchi]

Donc la dérivée première était (on a le droit de simplifier parce que le domaine de définition c'est x>3 donc on sait que x est positif.
On dérive donc la fraction comme un u/v en (u'v-v'u) / v²