Dérivée coriace !

[Peter57]

Bonjour à tous !
je suis très ennuyé par la recherche de la dérivée d'une fonction de type
Y = x ^(c + dx + ex2) avec ^= à la puissance.
(je ne sais pas comme faire les exposants :triste: )

[mathelot]

Bonjour à tous !
je suis très ennuyé par la recherche de la dérivée d'une fonction de type
Y = x ^(c + dx + ex2) avec ^= à la puissance.
(je ne sais pas comme faire les exposants :triste: )

bonjour,
écrire
puis utiliser la formule de dérivée d'une exponentielle



se dérive via la formule de dérivée du produit: (uv)'=u'v+uv'

[ampholyte]

Bonjour,

Il faut se rappeler que :



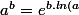Tu devrais pouvoir dériver plus facilement sachant que tu sais que :

[Peter57]

Merci !!!!
je ne savais pas en fait si et de quelle manière on pouvait appliquer la règle
(f(u))' = f'(u).u'
aux exponentielles.

[mathelot]

[tototo]

Bonjour à tous !
je suis très ennuyé par la recherche de la dérivée d'une fonction de type
Y = x ^(c + dx + ex2) avec ^= à la puissance.
(je ne sais pas comme faire les exposants :triste: )

Bonjour

(lnx * (c+dx+e*x^2))'=(1/x)*(c+...)+(lnx*(d+2ex))
Et( e^u)'=u'e^u

[Peter57]

Compris !

Merci à tous pour ce rappel de vieux vieux souvenirs !
mes années de lycée sont très loin !