Attention, le problème de départ fait intervenir des fonctions de R dans C, dont la définition de la dérivée est triviale (on dérive séparément partie réelle et partie imaginaire), tandis que la réponse de Chan79 parle de fonctions de C dans C, dont la définition de la dérivée est bien plus compliquée. En effet, avec la même définition que dans R, à savoir la limite du taux d'accroissement, on découvre avec horreur que plein de fonctions banales ne sont pas dérivables dans ce sens, par exemple la bonne vieille fonction z-->|z|² est représentée par un paraboloïde tout à fait régulier, ce qui laisserait à penser qu'elle est dérivable, or elle ne l'est en aucun point sinon 0. Même problème pour z-->Re(z) qui n'est dérivable nulle part, même pas en 0. (*)
Bref, la dérivée de a --> exp(ia) = cos(a) + i sin(a) est, par définition (on dérive séparément partie réelle et partie imaginaire) la fonction a --> -sin(a) + i cos(a) qui est en effet égal à i exp(ia). Puis pareil pour exp(-ia), ce qui permet en effet de retrouver que cos'=-sin. Mais ce n'est pas une nouvelle démonstration de cos'=-sin puisque ça utilise cos'=-sin (c'est caché dans la notation exponentielle, c'est tout). En tout cas pas besoin d'aborder l'analyse complexe ici.
-------------
(*) Pour la culture générale et parce que je me suis levé une heure trop tôt donc j'ai le temps :
Pour les fonctions de C dans C, il existe deux façons de dériver. La première façon, c'est la limite du taux d'accroissement, avec l'inconvénient que cette limite n'existe pas souvent parce qu'on peut tendre vers un certain z de multiples façons. Sur R, on a une limite à gauche et une limite à droite, point. Dans le plan complexe, on peut converger vers z en empruntant une infinité de chemins possibles. On peut tendre vers z à module constant (donc on tend vers l'argument de z) ou bien à argument constant (donc on tend vers le module de z) ou bien un mélange des deux... Les fonctions pour lesquels le taux d'accroissement admet une limite sont dites holomorphes. C'est la première façon de définir une "dérivée".
Il existe une deuxième façon, complètement indépendante, qui n'a rien à voir : les fonctions analytiques. Ce sont les fonctions développables en série entière. Par exemple exp(z) vaut

. Dans ce cas, on peut définir leur dérivée en dérivant terme à terme les
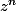
comme on le ferait avec un polynôme.
Il existe deux propriétés remarquables, que je trouve très belles (peut-être parce que je ne comprend pas tout - celui qui maîtrise parfaitement ce domaine doit trouver ça trivial) :
1) Les fonctions analytiques sont exactement les fonctions holomorphes (pourtant elles sont définies de façons très différentes !).
2) Les fonctions analytiques sont infiniment dérivables. Donc les holomorphes aussi, du coup, vu que ce sont les mêmes ! (Autrement dit : il suffit que ce soit une fois dérivable pour que ce le soit autant de fois qu'on veut. Pour les fonctions de R dans R - ou de R dans C, c'est pareil -, ce serait complètement faux.)
Les fonctions analytiques ont d'autres belles propriétés. Par exemple si deux fonctions analytiques coincident sur un certain domaine, même minuscule (mais plus grand qu'un point), elles coïncident partout. Ce genre de propriété n'existe pas pour les fonctions de R dans R, ce qui suggère une forme de supériorité de C.
D'ailleurs la définition "officielle" des fonctions usuelles fait intervenir les fonctions analytiques. Ainsi, le cosinus n'est pas défini comme le rapport côté adjacent sur hypothénuse ni comme l'abscisse du point du cercle unité correspondant à un angle, mais comme la partie paire de exp(iz), lequel est défini "officiellement" par la série ci-dessus (en terminale S on admet l'existence de l'exponentielle parce qu'on n'a pas le temps de faire un chapitre sur les fonctions analytiques, évidemment...)
Il resterait à parler de l'intégration complexe (si on définit des dérivées, inversement on va pouvoir parler d'intégrale). L'un des aspects les plus spectaculaires de cette notion, c'est son application au calcul d'intégrales dans R : pour intégrer entre a et b (réels), il est parfois plus simple de faire un détour dans le plan complexe (c'est la méthode des résidus). Encore une bonne raison de considérer que c'est C qui est le "vrai" ensemble, pas R qui n'est qu'un cas particulier.
