Démonstration d'une inégalité
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
bamans
- Membre Naturel
- Messages: 10
- Enregistré le: 08 Mar 2014, 13:37
-
 par bamans » 09 Mar 2014, 21:38
par bamans » 09 Mar 2014, 21:38
Bonjour, j'aimerai que vous m'aidiez sur une démonstration svp .
On me demande de prouver que pour tout élément h de [
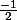
;0] : 0

g(1+h) - g(1) +h/2


.
Avec g(x)=
})
défini ]0;1] et f(x)=

défini dans ]0;1[,et aussi h

[-1/2;0].
Merci d'avance.

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 09 Mar 2014, 22:43
par Sa Majesté » 09 Mar 2014, 22:43
J'imagine que c'est plutôt g(1+h/2) ?
Il faut remplacer g par son expression avec f
Pour le côté gauche de linégalité c'est simple
Pour le côté droit, je suppose qu'on t'a donné des indications
-
bamans
- Membre Naturel
- Messages: 10
- Enregistré le: 08 Mar 2014, 13:37
-
 par bamans » 09 Mar 2014, 23:12
par bamans » 09 Mar 2014, 23:12
Non pourtant c'est bien g(1+h),peut être que c'est une erreur du sujet..Et pour le coté droit ,il n'y a aucune indication sur la feuille .

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 10 Mar 2014, 21:47
par Sa Majesté » 10 Mar 2014, 21:47
Je disais : c'est plutôt g(1+h)-g(1+h/2) que g(1+h) - g(1) +h/2
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 54 invités