Démonstration : si X² = a; X1=-racine(a) et X2=racine(a)
15 messages
- Page 1 sur 1
Démonstration : si X² = a; X1=-racine(a) et X2=racine(a)
Bonjour tout le monde !
j'ai des problemes : j'admet que si X² = a (a>0) , l'équation admet 2 solutions :
1) -Racine(a)
2) Racine(a)
seulement j'ai un probleme : j'ai besoin de connaitre la démonstration de cette regle pour pouvoir le comprendre et le retenir :(
j'ai essayé mais en vain, quelqun pourrait me démontrer cette regle ??
merci d'avance
BONNE ANNEE !
j'ai des problemes : j'admet que si X² = a (a>0) , l'équation admet 2 solutions :
1) -Racine(a)
2) Racine(a)
seulement j'ai un probleme : j'ai besoin de connaitre la démonstration de cette regle pour pouvoir le comprendre et le retenir :(
j'ai essayé mais en vain, quelqun pourrait me démontrer cette regle ??
merci d'avance
BONNE ANNEE !
lapras a écrit:Bonjour tout le monde !
j'ai des problemes : j'admet que si X² = a (a>0) , l'équation admet 2 solutions :
1) -Racine(a)
2) Racine(a)
seulement j'ai un probleme : j'ai besoin de connaitre la démonstration de cette regle pour pouvoir le comprendre et le retenir
j'ai essayé mais en vain, quelqun pourrait me démontrer cette regle ??
merci d'avance
BONNE ANNEE !
Tu es comme moi, quoi :we:
Ce dont il faut se souvenir est de la valeur absolue.
Or, |a| = a si a>0, ou -a si a<0. Voila d'où vient les 2 solutions. Tu peux aussi le prouver en sens inverse, en disant que le carré d'un nombre est toujours positif, même si le nombre est négatif :zen:
Utiliser un bazooka pour tuer une mouche...
Le fait que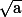 soit solution, ce n'est pas démontrable, puisque
soit solution, ce n'est pas démontrable, puisque 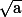 est défini comme ayant pour carré le nombre a.
est défini comme ayant pour carré le nombre a.
Ensuite,) est aussi solution car pour tout nombre x quelconque, (-x)²=x².
est aussi solution car pour tout nombre x quelconque, (-x)²=x².
Pour terminer, le théorème de d'Alembert nous permet d'affirmer qu'il n'y a pas d'autres solutions. (c'était mon petit coup de pistolet pour achever l'insecte)
:happy3:
Le fait que
Ensuite,
Pour terminer, le théorème de d'Alembert nous permet d'affirmer qu'il n'y a pas d'autres solutions. (c'était mon petit coup de pistolet pour achever l'insecte)
:happy3:
Non là je ne suis pas trop d'accord avec toi quand même. Parce que je pars de la forme générale ax²+bx+c=0 pour arriver à cette fameuse forme particulière ax²=c.
Et je ne vais pas refaire ici toute la démo avec la discriminant pour montrer que les solutions sont (-b-...) et (-b+...).
J'applique ensuite à ce cas général le fait que b soit nul et je trouve bien ce que l'on demande.
T'es pas d'accord ?
Et je ne vais pas refaire ici toute la démo avec la discriminant pour montrer que les solutions sont (-b-...) et (-b+...).
J'applique ensuite à ce cas général le fait que b soit nul et je trouve bien ce que l'on demande.
T'es pas d'accord ?
Le discriminant découle de la forme canonique.
C'est-à-dire qu'on est arrivé à l'équation :
^{2}=\frac{b^{2}-4ac}{4a^{2}})
A partir de là, le signe du numérateur est devenu important dans le sens où il apportait l'existence et le nombre de solutions de l'équation. Les solutions par contre elles viennent bien du fait que V(a) et -V(a) sont les racines du polynôme x²-a.
:happy3:
C'est-à-dire qu'on est arrivé à l'équation :
A partir de là, le signe du numérateur est devenu important dans le sens où il apportait l'existence et le nombre de solutions de l'équation. Les solutions par contre elles viennent bien du fait que V(a) et -V(a) sont les racines du polynôme x²-a.
:happy3:
15 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 83 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
