[TS] Démonstration par récurrence d'une dérivée nième.

[twenty]

Bonjour/Bonsoir.

J'ai le DM suivant à réaliser :

Soit f la fonction définie sur R par f(x) = cos(2x), démontrer que pour tout n € N* :
f^n(x)= (2^n)*cos(2x + n*(Pi/2))

Plusieurs problèmes se posent pour moi :

- Je ne sais pas faire des dérivées n-ièmes.
- Je ne sais pas dériver cos 2x... Une simple fonction composée suffirait-elle ?


Je pensais dériver cos 2x et montrer que cette dérivée équivaut à f^1(x) pour l'initialisation.

Cependant je ne sais pas trop comment faire mon hérédité !

Bonne soirée.

[twenty]

A lock, j'ai réussi à trouver la solution avec beaucoup de rigueur.

Désolé d'avoir posté pour trouver deux minutes après mais je galérais depuis plusieurs heures. Comme vous pouvez le voir je ne poste pas à la légère :p Mon dernier poste date d'il y a un an.

Bonne soirée.

[Dinozzo13]

Salut !

Pour l'exercice, il n'est pas nécessaire de savoir calculer une dérivée -ième puisqu'elle t'est donnée.
Tu as juste à le montrer par récurrence.
Initialisation : Si alors en sachant que est la fonction composée de 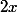pas .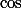

Sachant que la dérivée de est , tu peux montrer que .

Une fois l'initialisation faite, suppose qu'il existe un rang tel que , montre qu'alors .
.

[Dinozzo13]

A lock, j'ai réussi à trouver la solution avec beaucoup de rigueur.

Désolé d'avoir posté pour trouver deux minutes après mais je galérais depuis plusieurs heures. Comme vous pouvez le voir je ne poste pas à la légère :p Mon dernier poste date d'il y a un an.

Bonne soirée.

Ah ok :+++:

[geegee]

Bonjour/Bonsoir.

J'ai le DM suivant à réaliser :

Soit f la fonction définie sur R par f(x) = cos(2x), démontrer que pour tout n € N* :
f^n(x)= (2^n)*cos(2x + n*(Pi/2))

Plusieurs problèmes se posent pour moi :

- Je ne sais pas faire des dérivées n-ièmes.
- Je ne sais pas dériver cos 2x... Une simple fonction composée suffirait-elle ?


Je pensais dériver cos 2x et montrer que cette dérivée équivaut à f^1(x) pour l'initialisation.

Cependant je ne sais pas trop comment faire mon hérédité !

Bonne soirée.

cos'2x=-2sin2x