[ts] demonstation Fct ln

[Lalyo]

Bonjour j´ai un petit exercice que je n´arrive pas a faire, si quelqu´un voulait bien m´aider, je lui en serait reconnaisant.

1.Démontrer que pour tout réel u>-1 , ln(1+u)
2.En deduire que pour tout entier n>1, ln(1+1/n)<1/n et obtenir (1+1/n)^n>e


3.a)De la même facon démontrer que pour tout entier n>2 (1-1/n)^-n>e

b)Démontrer à partir de cela que pour tout entier n>1, e<((n+1)/n)^(n+1)

4.Obtenir à l´aide des questions 3.a) et 3.b) l´encadrement: pour tout entier n>1,

((n+1)/n)^n
5.V est la suite définie pour tout entier n>1 par: Vn=((n+1)/n)^n

a) démontrer que pour tout entier n>1, 0
b) en déduire que la suite v converge vers e

Merci d´avance pour votre aide






Pour la 1) à part faire l´étude de la fonction x -> x - ln(1 + x) je ne vois pas. je voudrais savoir si ce raissoment est juste

2) Application directe, la fonction exp étant croissante

3) démarche analogue en remplaçant u par -1/n dans la formule démontrée en 1)

là aussi je voudrais savoir si c'est juste

merci encore

[Flodelarab]

Bonjour j´ai un petit exercice que je n´arrive pas a faire, si quelqu´un VOULAIT bien m´aider, je lui serait reconnaisant.

Rien que pour ça, je ne participerais pas.

[amine801]

slt
moi ca me derange pas de participer :we:
tu connais les integrales?

[Lalyo]

désolé, j'ai pas eu le temps de me relire

pour les integrales, j'ai pas en vu ça en cours donc désolé

[amine801]

alors oblige la methode moin sympa il faut etudier la fonction
u->u-ln(1+u) et demontré quelle est positif
sur l'intervalle en question :we:

[Lalyo]

donc j'étudie la fonction x - ln(1 + x) pour savoir quand elle est supérieur a zéro, C'est bien cela ??

[amine801]

oui c'est cela sur l'intervalle en question

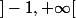
[Lalyo]

oki, et pour les autres propositions que je propose pour les autres questions, elles sont justes ??