paquito a écrit:Bonjour Waax
Tu as résolu sans problème cet exo, mais j'ai fait une faute de frappe et mis l'inégalité dans le mauvais sens et les entiers ne sont pas forcément consécutifs; donc le nouvel énoncé devient:
Déterminer tous les entiers:

tels que:

Ca te fait deux exos pour le prix d'un seul! :we:
On peut dire que je suis gâté ! :lol3:
Si j'ai pris en compte uniquement le cas où les entiers sont successifs, c'est plus pour arriver à y voir clair pour le cas général (car il me semble évident qu'il existe une infinité de solutions pour le premier exercice..!).
Pour le second exercice, je dirais au contraire que le nombre de solutions est fini, même s'il semble grand..!
Je l'ai vu ce matin mais je n'ai pas eu le temps de m'y pencher vraiment. On peut juste dire que lorsque le couple
)
est suffisamment grand (donc lorsque
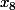
l'est), l'inéquation n'admet aucunes solutions. Il faut encore prouver ce que j'avance (ce qui ne risque pas d'être trop difficile) mais surtout de déterminer la plus petite valeur de
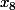
pour laquelle l'inéquation n'a pas de solutions. Puisque

, cela revient à trouver la valeur de
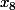
pour laquelle on a:
(1)
)
Puisque la somme de gauche dans 1 est maximale lorsque tous les
_{0 \leq i \leq 7})
sont maximaux, on en déduit que:
(2)

Ou encore:
(3)

On a finalement l'inéquation:
(I)

Résolvons (I) en étudiant le signe du trinôme

. Son discriminant étant
^2-4*72=112)
,
On en déduit que le trinôme est du signe opposé au coefficient de son monôme dominant, soit négatif, lorsque
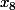
est compris entre ses deux racines réelles
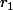
et
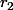
, définies par:

et

Or, puisque tous les entiers
_{0 \leq i \leq 9})
sont distincts, non nuls, et rangés dans l'ordre croissant, on en déduit que

. Autrement dit, l'inéquation n'admet des solutions que lorsque
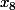
est compris entre 9 et 15.
Remarquons maintenant que l'ensemble des solutions de l'inéquation originelle lorsque
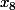
est fixé est le même que l'inéquation suivante:
)
 +x_9 \geq \frac{x_8 x_9}{2})
En effet, on recherche à chaque fois un encadrement de
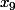
pour lequel l'inéquation est vérifiée, autrement dit, plus la somme de gauche est grande, plus cet encadrement est grand, et donc on déduit que l'encadrement qui donne toutes les valeurs de
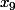
pour lesquelles l'inéquation est vérifié est celui où la somme de gauche est maximale, à savoir lorsque les
_{0\leq i \leq 7})
sont maximaux, donc lorsque ces mêmes entiers sont les 8 entiers successifs inférieurs à
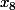
.
On en déduit alors que l'équation
)
admet toutes les solutions de l'inéquation originelle pour
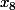
fixé.
On remarque que
)
s'écrit aussi:
)

.
On applique alors l'inégalité
)
pour chaque valeur possible de
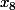
, à savoir 9, 10, 11, 12, 13, 14 et 15. On note

l'ensemble des valeurs de
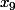
pour lesquelles le 10-uplet
)
est solution de l'inéquation
)
pour chacune des valeurs précédente. On a alors:
- Pour
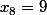
,

, donc on a

.
- Pour
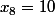
, on a

, donc a

- Pour
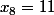
, on a

, donc a

.
- Pour
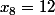
, on a

, donc a

.
- Pour
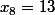
, on a

, donc a

puisque

.
- Pour
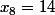
, on a

, donc a

puisqu'on a

.
- Pour
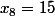
, on a

, donc a

puisqu'on a

.
On en déduit l'ensemble S des solutions de l'inéquation de l'exercice (où on note
_{0 \leq i \leq 7})
, une famille quelconque d'entiers strictement positifs, distincts et strictement inférieurs au deux derniers éléments de chaque ensemble solution) est défini par:
; (x_1; x_2; ...; x_7; 9; 11);)
; (x_1; x_2; ...; x_7; 10; 11); (x_1; x_2; ...; x_7; 10; 12);(x_1; x_2; ...; x_7; 10; 13); (x_1; x_2; ...; x_7; 11; 12);)
; (x_1; x_2; ...; x_7; 12; 13)])
EDIT: En fait c'est en réfléchissant au problème que ça m'est venu, donc s'il y a une erreur de calcul, j'en suis désolé, réfléchir devant un écran d'ordinateur m'a quelque peu fatigué.. En tout cas j'espère que c'est lisible.. Et bonne soirée :we:
définie par
et pour tout
dans
:
[/CENTER]
