Demande d'exercices - PGCD, Bézout, Gauss

[upium666]

Bonjour à tous et à toutes !

Je suis à la demande d'exercices intéressants concernant le PGCD, le théorème de Bézout, le théorème de Gauss, et si possible des exercices qui font intéragir ces trois notions entre elles
Des exercices du type :

o On note n un naturel non nul, A l'entier 3n+1 et B l'entier 5n-1
a)Montrer que le PGCD de A et B est un diviseur de 8
b)Pour quelles valeurs de n ce PGCD est-il égal à 8 ?

o Montrer en vous servant absolument du théorème de Bézout que si x et y sont des entiers premiers entre eux, il en est de même des entiers 3x+4y et 4x+5y

etc...
Des exercices qui demandent de la réflexion quoi, et pas que du cours

Merci

[chan79]

salut
j'ai vu passer cet exo récemment sur maths-forum:
si n est un entier naturel non nul, on pose:
a=11n+3
b=13n-1
Déterminer les valeurs de n pour lesquelles le PGCD de a et b est 50.
Exemple:
si n=27 alors a=300 et b=350 et le GGCD de 300 et 350 est 50
C'est un exo pas si évident à moins qu'un truc simple ne m'ait échappé...

[upium666]

salut
j'ai vu passer cet exo récemment sur maths-forum:
si n est un entier naturel non nul, on pose:
a=11n+3
b=13n-1
Déterminer les valeurs de n pour lesquelles le PGCD de a et b est 50.
Exemple:
si n=27 alors a=300 et b=350 et le GGCD de 300 et 350 est 50
C'est un exo pas si évident à moins qu'un truc simple ne m'ait échappé...

[chan79]

c'est bien ça
une démo ?

[Ben314]

Au "RugBall" (c'est un nouveau sport...) on peut marquer des "buts" rapportant 15 points et des "essais" rapportant 8 points.
Montrer que tout les score supérieurs à une certaine valeur sont réalisable et déterminer quel est le plus grand score non réalisable.

Généralisation au cas où les "buts" rapportent A points et les "essais" B points (A,B entier naturels)

[upium666]

c'est bien ça
une démo ?

Je ne la trouve pas très rigoureuse :

a=11n+3
b=13n-1
PGCD(a,b)=50

50/a et 50/b

alors :



Par somme :



a=11n+3=275u+25
b=13n-1=325u+25





On remplace dans


J'ai dit que ce n'est pas rigoureux car à aucun moment je n'ai parlé de PGCD et j'ai l'impression que je n'ai fait qu'avoir eu du bol dans cet exemple ... :s

[Ben314]

a=11n+3 ; b=13n-1 ; Déterminer les valeurs de n pour lesquelles le PGCD de a et b est 50.

perso, j'aurais écrit (comme l'algo d'euclide) que :
pgcd(13n-1,11n+3)=pgcd(11n+3,2n-4)=pgcd(2n-4,n+23)=pgcd(n+23,-50)
Qui vaut 50 ssi n+23 est divisible par 50.

[upium666]

Au "RugBall" (c'est un nouveau sport...) on peut marquer des "buts" rapportant 15 points et des "essais" rapportant 8 points.
Montrer que tout les score supérieurs à une certaine valeur sont réalisable et déterminer quel est le plus grand score non réalisable.

Généralisation au cas où les "buts" rapportent A points et les "essais" B points (A,B entier naturels)

Je le trouve assez dur cet exercice, merci :p
Je vais y réfléchir

[upium666]

perso, j'aurais écrit (comme l'algo d'euclide) que :
pgcd(13n-1,11n+3)=pgcd(11n+3,2n-4)=pgcd(2n-4,n+23)=pgcd(n+23,-50)
Qui vaut 50 ssi n+23 est divisible par 50.

C'est vrai, c'est plus simple

[chan79]

C'est vrai, c'est plus simple

On peut aussi se demander pour quelles valeurs de n le PGCD est 25.

[Ben314]

On peut aussi se demander pour quelles valeurs de n le PGCD est 25.

ssi pgcd(n+23,50)=25, c'est à dire n+23=25+50k avec k entier.

[Ben314]

Sinon (tiré d'un autre post), tu peut regarder si tu sait comment t'y prendre pour résoudre ça :
6x+10y+15z=7 avec x,y,z entiers relatifs.
C'est pas super dur... mais pas super évident non plus...

[upium666]

Sinon (tiré d'un autre post), tu peut regarder si tu sait comment t'y prendre pour résoudre ça :
6x+10y+15z=7 avec x,y,z entiers relatifs.
C'est pas super dur... mais pas super évident non plus...

J'y avais pensé, mais je n'ai pas la technicité pour résoudre des équations diophantiennes du premier ordre à 3 inconnues

En fait, je pense que pour résoudre votre problème du RugBall, il faut montrer que :


et

et déterminer le plus petit c qui vérifie cette condition
Dans ce cas, le plus grand nombre non réalisable serait c-1 car à partir de ce c on peut obtenir tous les nombres qu'on veut

Mais pour cela, il faut savoir résoudre les équations diophantiennes du premier ordre à 3 inconnues :s

De l'aide ?

[Ben314]

Pour le rugball, a mon avis, le plus simple, c'est de commencer par faire... ce qu'on sait faire, c'est à dire résoudre 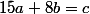dans Z.
Après, il faut regarder (pour c fixé) s'il y a ou pas des solutions dans N : tu peut commencer par des exemples c=20 ? c=40 ? c= 12 ? etc
Normalement aprés quelques essais, tu devrais voir comment montrer qu'à partir d'une certaine taille (pour c), il y a forcément des solutions dans N.

Enfin, la partie pas totalement évidente, c'est de trouver le max non atteignable : dans un cas concret (comme ici avec 15 et 8), on peut tatoner vu qu'on a déjà une barre à partir de laquelle on sait que ça marche pour tout les entiers c.
Mais il y a aussi une jolie astuce qui donne directement le résultat avec peu de calcul (mais il faut de toute façon commencer par résoudre l'équation dans Z)

[upium666]

Pour le rugball, a mon avis, le plus simple, c'est de commencer par faire... ce qu'on sait faire, c'est à dire résoudre dans Z.
Après, il faut regarder (pour c fixé) s'il y a ou pas des solutions dans N : tu peut commencer par des exemples c=20 ? c=40 ? c= 12 ? etc
Normalement aprés quelques essais, tu devrais voir comment montrer qu'à partir d'une certaine taille (pour c), il y a forcément des solutions dans N.

Enfin, la partie pas totalement évidente, c'est de trouver le max non atteignable : dans un cas concret (comme ici avec 15 et 8), on peut tatoner vu qu'on a déjà une barre à partir de laquelle on sait que ça marche pour tout les entiers c.
Mais il y a aussi une jolie astuce qui donne directement le résultat avec peu de calcul (mais il faut de toute façon commencer par résoudre l'équation dans Z)

Des amis m'ont dit que a et b peuvent être négatifs, est-ce vrai ?

[Ben314]

Des amis m'ont dit que a et b peuvent être négatifs, est-ce vrai ?

Normalement, pour le "RugBall" (qui, à ma connaissance n'est pas un jeu qui existe...), le nombre d'essais et de buts marqués sont forcément positif. (Je regarde jamais le foot, mais j'ai cru comprendre que O.M / P.S.G. = 3 / -5 , c'était pas trop possible...)

Ce que te dit "la théorie" (que tu as commencé à voir en cours), c'est que, vu que pgcd(15,8)=1, quelque soit la valeur de c dans Z, l'équation aura des solutions... dans Z.
Le but de l'exercice, c'est de voir à quelle condition (sur c) il y a des solutions dans N.
Par exemple, avec des "buts" à 15 points et des "essais" à 8 points, tu n’arrivera jamais à marquer exactement 20 points...

[upium666]

Normalement, pour le "RugBall" (qui, à ma connaissance n'est pas un jeu qui existe...), le nombre d'essais et de buts marqués sont forcément positif. (Je regarde jamais le foot, mais j'ai cru comprendre que O.M / P.S.G. = 3 / -5 , c'était pas trop possible...)

Ce que te dit "la théorie" (que tu as commencé à voir en cours), c'est que, vu que pgcd(15,8)=1, quelque soit la valeur de c dans Z, l'équation aura des solutions... dans Z.
Le but de l'exercice, c'est de voir à quelle condition (sur c) il y a des solutions dans N.
Par exemple, avec des "buts" à 15 points et des "essais" à 8 points, tu n’arrivera jamais à marquer exactement 20 points...

Justement, j'ai cru mal comprendre l'exercice :
Je pense jusqu'à maintenant qu'il existe un certain c à partir duquel on peut obtenir tous nombres supérieurs ou égaux à c rien qu'en disposant des 15 et des 8 de certaines manières précises, mais je suis persuadé que c'est une fausse approche
En fait, je ne crois pas avoir très bien compris ce qu'il faut démontrer ou trouver :s

[Ben314]

Je pense jusqu'à maintenant qu'il existe un certain c à partir duquel on peut obtenir tous nombres supérieurs ou égaux à c rien qu'en disposant des 15 et des 8 de certaines manières précises.

C'est bien ça qu'il faut démontrer, c'est à dire que pour tout les c supérieurs à ??? l'équation 15x+8y=c aura des solutions non seulement dans Z, mais aussi dans N (i.e. positives ou nulles)

Si tu ne vois pas trop quoi faire, commence par exemple par résoudre "normalement" (c'est à dire dans Z) l'équation 15x+8y=100 puis regarde s'il y a des solutions avec x et y positifs (et si oui, combien y en a-t-il ?)

[upium666]

C'est bien ça qu'il faut démontrer, c'est à dire que pour tout les c supérieurs à ??? l'équation 15x+8y=c aura des solutions non seulement dans Z, mais aussi dans N (i.e. positives ou nulles)

Si tu ne vois pas trop quoi faire, commence par exemple par résoudre "normalement" (c'est à dire dans Z) l'équation 15x+8y=100 puis regarde s'il y a des solutions avec x et y positifs (et si oui, combien y en a-t-il ?)

Il me faut déterminer une solution particulière de 15a+8b=c, je n'y arrive pas :/

[Ben314]

Il me faut déterminer une solution particulière de 15a+8b=c, je n'y arrive pas :/

L'ago. d'euclide "étendu" (ou bien un petit peu d'inspiration...) te donnent une solution de 15a+8b=1.
Tu n'a plus qu'à multiplier à la fois le 'a' et le 'b' de ta solution par c pour avoir une solution de 15a+8b=c (c'est pas forcément la "plus belle", mais... c'est une solution...)