Voici mon raisonement :
quand on pose X=x/2 , x tend vers 0 implique que X tend vers 0
on obtient :
On a pour tout x > 0 ,
Comme
Bon par contre la 4 je suis encore en train de la faire j'attend vos remarque avec impatience.
(Correction)Limites 1ere S
15 messages
- Page 1 sur 1
(Correction)Limites 1ere S
par Kiritsugu » 10 Fév 2016, 14:35
Bonsoir je vous sollicite pour m'aider dans la correction de quelques limites , merci :
}{x^2} })
))
sin(\frac{1}{x-1}))
.
Voici mon raisonement :
}{x^2} = \lim_{x\to 0}(\frac{sin(\frac{x}{2})}{\frac{x}{2}}}.\frac{\frac{x}{2}}{x^2}.\frac{sin\frac{x}{2}}{\frac{x}{2}}.\frac{\frac{x}{2}}{1}))
quand on pose X=x/2 , x tend vers 0 implique que X tend vers 0
on obtient :
.\lim_{x \to 0 }\frac{x}{2x^2}.\frac{x}{2} = \lim_{x \to 0}\frac{x^2}{4x^2}=\frac{1}{4})
On a pour tout x > 0 ,
> 1(cos 0 = 1) \Rightarrow -cos(\frac{1}{\sqrt{x}})< -1 \Rightarrow 1-cos(\frac{1}{\sqrt{x}})< 0 \Rightarrow x(1-cos(\frac{1}{\sqrt{x}})< 0)
Comme
alors la propriete de minoration nous permet d'ecrire :
) = 0)
.
Bon par contre la 4 je suis encore en train de la faire j'attend vos remarque avec impatience.
Voici mon raisonement :
quand on pose X=x/2 , x tend vers 0 implique que X tend vers 0
on obtient :
On a pour tout x > 0 ,
Comme
Bon par contre la 4 je suis encore en train de la faire j'attend vos remarque avec impatience.
Re: (Correction)Limites 1ere S
par zygomatique » 10 Fév 2016, 14:46
salut
1/ justifier l'avant dernière inégalité ...
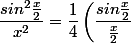2/ tu te compliques inutilement ::^2)
3/ faux ...
utilise plutôt cos t = cos [2(t/2)] = ....
4/ pour tout réel u non nul :
1/ justifier l'avant dernière inégalité ...
2/ tu te compliques inutilement ::
3/ faux ...
utilise plutôt cos t = cos [2(t/2)] = ....
4/ pour tout réel u non nul :
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: (Correction)Limites 1ere S
par Carpate » 11 Fév 2016, 08:33
Et qu'as-tu obtenu quand tu "as refait la 3" ?
Re: (Correction)Limites 1ere S
par zygomatique » 11 Fév 2016, 12:21
Carpate a écrit:3) Tu pourrais utiliser :=2sin^2(\frac{1}{2\sqrt{x}}))
et
il me semble préférable d'utiliser cos(2a) ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: (Correction)Limites 1ere S
par Carpate » 11 Fév 2016, 13:23
Affaire de goût.
Pourtant = 2 cos^2(\frac{a}{2}))
est bien tiré de  = ....)
Pourtant
Re: (Correction)Limites 1ere S
par zygomatique » 11 Fév 2016, 16:42
Carpate a écrit:Affaire de goût.
Pourtant
disons que c'est plutôt 1 - cos a ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: (Correction)Limites 1ere S
par Carpate » 11 Fév 2016, 18:03
Honte à moi !
Je fais deux fois cette grave faute de frappe sans la voir !
C'est pourquoi je n'avais pas saisi ta première remarque.
Donc je rectifie, pour Kiritsugo :
=2 sin^2(\frac{1}{2\sqrt{x}}))
Je fais deux fois cette grave faute de frappe sans la voir !
C'est pourquoi je n'avais pas saisi ta première remarque.
Donc je rectifie, pour Kiritsugo :
Re: (Correction)Limites 1ere S
par Kiritsugu » 11 Fév 2016, 20:23
Bon après avoir essayer d refait la 3 avec vos remarquer quand j'arrive a lim(2)
je ne voit pa comment faire a part les propriété de majoration , minoration ou l théorème des gendarmes vous n'avez pas d'autres démarches.
Re: (Correction)Limites 1ere S
par Carpate » 12 Fév 2016, 11:08
Il faut faire apparaître un terme de la forme : }{u})
qui tend vers 1 quand u tend vers 0
rappel :=2sin^2(\frac{1}{2\sqrt{x}}))
application de=2sin^2(a))
formule tirée de=cosa cosb -sina sinb)
, avec a=b, et de 
Il faut exprimer x en fonction de
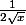
^2 = \frac{1}{4x})
^2})
)=\frac14 (\frac{1}{(\frac{1}{2\sqrt{x}})^2}) (2sin^2(\frac{1}{2\sqrt{x}}))=\frac12(\frac{sin(\frac{1}{2\sqrt{x}})}{\frac{1}{2\sqrt{x}}})^2)
qui tend vers 
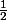
quand 
rappel :
application de
formule tirée de
Il faut exprimer x en fonction de
Re: (Correction)Limites 1ere S
par Kiritsugu » 12 Fév 2016, 12:24
Merci beaucoup j'y vois plus clair maintenant.
Re: (Correction)Limites 1ere S
par Kiritsugu » 12 Fév 2016, 12:30
Mais comment vous faites pour avoir ce genre de coup d'œil ?
Re: (Correction)Limites 1ere S
par Carpate » 12 Fév 2016, 13:27
La clé de ces 4 exercices est l'utilisation de la limite en 0 de
Ca te donne le but des calculs à réaliser : faire apparaître une telle fonction u.
Tu peux ne pas la trouver du premier coup mais après quelques tâtonnements ...
Ca te donne le but des calculs à réaliser : faire apparaître une telle fonction u.
Tu peux ne pas la trouver du premier coup mais après quelques tâtonnements ...
15 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :