Correction exercice de géométrie

[skertel]

Bonjour à tous. Je ne comprends pas toute la correction d'un exercice de géométrie).

Voici l'énoncé (c'est la troisième question d'un exercice) (il y a un triangle ABC, avec a côté opposé au sommet A, et x l'angle au sommet A; pareil pour b et y etc...)

On appelle A3 le milieu du segment [BC], B3 le milieu du segment [AC] et C3 le milieu du segment [AB].
a) Montrer que le triangle A3B3C3 est semblable au triangle ABC.
b) En déduire que les médiatrices du triangle ABC sont concourantes en un point O dont les coordonnées
barycentriques par rapport aux points A; B; C sont données par
O = bar ((A; a cosx)(B; b cosy )(C; c cosz))

C'est ok pour la première question, par contre, la compréhension de la correction de la b) me pose problème.

Correction: b)
Comme les médiatrices du triangle ABC sont les hauteurs du triangle A3B3C3, ces droites sont concourantes
en un point O de coordonnées barycentriques
O =bar{(A3, (a/2)cosycosz)(B3,(b/2)cosxcosz)(C3, (c/2)cosxcosy)}

En utilisant l'associativité des barycentres, on en déduit que
O = bar {(B,acosycosz)(C,acosycosz)
(A,bcosxcosz)(C,bcosxcosz)
(A,ccosxcosy)(B,ccosxcosy)}

(puis factorisation ...)
En, en utilisant la formule d'Al-Kashi, on a....................... la réponse.



La partie rouge est obtenue à partir d'un résultat précédent et je comprends cette partie.
Par contre, je ne vois pas comment on passe de la partie rouge à la partie bleue.

Je précise que cet exercice est un devoir de vacance ( :marteau: ) pour une prépa math sup, donc le niveau est entre lycée et supérieur.

Merci beaucoup d'avance pour votre aide

[busard_des_roseaux]

Bj,

à vue de nez:

A3B3C3 est le triangle médian de ABC.

D'après des théorèmes de droites de milieu, A3B3C3 a ses côtés
parallèles à ceux de ABC et de longueurs moitié

Ils sont semblables donc de mêmes angles

Les médiatrices de ABC sont hauteurs de A3B3C3 donc concourantes

Ensuite , les hauteurs dans le triangles médian A3B3C3 découpent
les côtés perpendiculaires selon des longueurs obtenues avec des cosinus.

Le théorème d'associativité permet d'écrire H de A3B3C3
(H de A3B3C3 = O de ABC) comme barycentre avec comme "poids"
des cosinus d'angles.

[busard_des_roseaux]

Je précise que cet exercice est un devoir de vacance ( :marteau: ) pour une prépa math sup, donc le niveau est entre lycée et supérieur.

niveau 1èreS pour la question (3)

[skertel]

Le théorème d'associativité permet d'écrire H de A3B3C3
(H de A3B3C3 = O de ABC) comme barycentre avec comme "poids"
des cosinus d'angles.

Tu pourrais détailler le théorème de l'associativité entre le premier O (rouge) et le deuxième (bleu), c'est là que je galère à voir le pourquoi du comment.

Le reste, avec le théorème des milieux etc, c'était plutôt pour la première question, j'avais assez bien compris.

[busard_des_roseaux]

Tu pourrais détailler le théorème de l'associativité entre le premier O (rouge) et le deuxième (bleu), c'est là que je galère à voir le pourquoi du comment.

Le reste, avec le théorème des milieux etc, c'était plutôt pour la première question, j'avais assez bien compris.

et ben, dans le triangle médian A3B3C3

la hauteur issue de A3 découpe le côté opposé B3C3
en deux avec des longueurs à calculer

mais:

par similitude
et

[skertel]

Je crois que tu vois pas où est mon problème.

Le truc que je vois pas, c'est comment tu obtiens ça:
En utilisant l'associativité des barycentres, on en déduit que
O = bar {(B,acosycosz)(C,acosycosz)
(A,bcosxcosz)(C,bcosxcosz)
(A,ccosxcosy)(B,ccosxcosy)}

à partir de ça: O =bar{(A3, (a/2)cosycosz)(B3,(b/2)cosxcosz)(C3, (c/2)cosxcosy)}


Je vois pas du tout le rapport entre les deux... :s

[busard_des_roseaux]

je t'explique avec mes mots :hum:

i) le triangle médian A3B3C3 est la réduction (de moitié) de ABC

ii)
Dans le triangle A3B3C3,
notons le pied de perpendiculaire de A3 sur le coté opposé B3C3

La longueur B3A3" est la moitié de BH=c cos(B)

Donc on récupère
comme barycentre de B3(b cos(C)) et C(c cos(B))
que l'on écrit,
les coefficients étant définis à un coefficient multiplicatif près:


barycentre de B3(b cos(C)cos(A)) et C3(c cos(B)cos(A))

et donc O va être barycentre de
A3( acos(C)cos(B)) B3(b cos(C)cos(A)),C3(c cos(B)cos(A))

et après tu peux reporter la moitié des poids de A3
de chaque côté sur les sommets B et C

ou alors l'homothétie de centre G et de coefficient -1/2 envoie
ABC sur A3B3C3 et H sur O
en conservant les barycentres

[busard_des_roseaux]

Bj,

soit ABC triangle avec O,H,G
O centre du cercle circonscrit,H orthocentre, G centre de gravité

A1,B1,C1 les pieds des hauteurs
A3,B3,C3 les pieds des médianes

On calcule les distances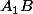 et




donc bar
bar

par permutation
bar

l'homothétie de centre G et de rapport -1/2 conserve les coefficients
barycentrique et envoie H sur O

bar

Comme A3,B3,C3 sont les milieux des côtés, on répartit les
coefficients de O, fifty-fifty , sur les sommets A,B,C

bar

Aevc la loi de sinus

bar

bar


bar


bar