[TS+] Convergence vers 1/e
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 22 Fév 2010, 17:49
par benekire2 » 22 Fév 2010, 17:49
Bonsoir, tout à l'heure je regardais les suites qui converge vers pi, ou e et je suis tombé sur celle ci :
^{\frac{1}{n}}}{n})
qui converge vers 1/e
Il me semble que la démonstration est abordable au niveau lycée, si quelqu'un sait comment procéder, peut-il me le dire?
Merci :id:
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 22 Fév 2010, 19:28
par benekire2 » 22 Fév 2010, 19:28
Up :ruse:
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 22 Fév 2010, 20:16
par Skullkid » 22 Fév 2010, 20:16
Salut, tu es sûr que la démo est niveau lycée ? J'ai pas vraiment cherché à poser les calculs, mais comme ça mélange des factorielles et des puissances qui dépendent de n, ça me semble difficile de s'en sortir qu'avec des méthodes de lycée...
En méthode bulldozer y a la formule de Stirling, qui donne le résultat assez facilement.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 22 Fév 2010, 23:08
par Nightmare » 22 Fév 2010, 23:08
Une méthode presque abordable niveau lycée :
=\frac{1}{n}\(ln(n!)-nln(n)\)=\frac{1}{n}\Bigsum_{k=1}^{n} ln\(\frac{k}{n}\))
et on reconnait presque une somme de Riemann (bon en fait il faut justifier que ça converge vers
dx)
et c'est effectivement loin d'être de niveau term, même pas sup a priori)

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 22 Fév 2010, 23:25
par Ben314 » 22 Fév 2010, 23:25
Salut,
Je suis pas certain que l'on ait besoin de "la formule de stirling en entier", mais seulement du début...
Il me semble que le théorème suivant :
[quote] Si une suite de réels strictement positifs Un est telle que
U(n+1)/Un tend vers L alors :
- Si L>1 alors Un tend vers l'infini
- Si L0 fixé, quoicéti qu'on trouve ....
Il me semble que c'est suffifant pour trouver la limite de Benekire (sinon, on peut raffinner le théorème ci dessus pour traiter le cas L=1 et les sous cas selon l'équivalent de ( U(n+1)/Un - 1 ) mais ça fait nettement moins "terminale"...)
EDIT : je confirme qu'il n'y as pas besoin de plus que le théorème ci dessus pour trouver la "limite de Benekire".
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 23 Fév 2010, 02:34
par Zweig » 23 Fév 2010, 02:34
c'est effectivement loin d'être de niveau term, même pas sup a priori)
Si si, c'est niveau Sup, je les ai vues cette année (démos à l'appui), même la formule plus générale des Sommes de Riemann, avec les sigma et tout.
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 23 Fév 2010, 10:33
par benekire2 » 23 Fév 2010, 10:33
Je reste même totalement convaincu qu'il existe une preuve entièrement niveau TS ( bon niveau quand même)
Je continue de chercher ...
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 23 Fév 2010, 11:11
par benekire2 » 23 Fév 2010, 11:11
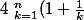^k \le e^n \le \Bigprod_{k=1}^{n}(1+\frac{1}{k})^{k+1})
On réécrit (si je ne me suis pas trompé) :
^n}{n!} \le e^n \le \frac{(n+1)^{n+1}}{n!})
Ça y est c'est mieux comme ça, il me semble que l'on peut se servir de ça ... mais comment ? Je cherche encore...
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 23 Fév 2010, 11:22
par Nightmare » 23 Fév 2010, 11:22
Zweig a écrit:Si si, c'est niveau Sup, je les ai vues cette année (démos à l'appui), même la formule plus générale des Sommes de Riemann, avec les sigma et tout.
Je maintiens que ce n'est pas au programme au sens où ln n'est pas définie partout sur [0,1], ce n'est donc pas une vraie somme de Riemann et il faut donc justifier la convergence de la somme vers l'intégrale et ce n'est pas trivial.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 23 Fév 2010, 11:27
par Ben314 » 23 Fév 2010, 11:27
benekire, la preuve que je t'ais proposé ne te convient pas ? :cry:
(je peut détailler, mais telle quel, tu devrait trouver...)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 23 Fév 2010, 11:39
par benekire2 » 23 Fév 2010, 11:39
J'avais même pas vu ... :triste:
Oui elle convient, mais c'est pas un théorème de TS si je ne m'abuse ?
Enfin, moi je recherche THE preuve totalement niveau Lycée...
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 23 Fév 2010, 12:00
par Nightmare » 23 Fév 2010, 12:00
L'exercice n'est pas de niveau TS. Par contre, on peut le résoudre en utilisant seulement le outils de TS, Cf l'esquisse de preuve de Ben.
:happy3:
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 23 Fév 2010, 12:08
par benekire2 » 23 Fév 2010, 12:08
certes, il n'est pas de niveau TS, mais je suis convaincu qu'il existe une preuve plus simple que celle du ben ,
d'ailleurs mon début de raisonnement qui aboutit à une inégalité je reste persuadé qu'il peut mener à la démo.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 23 Fév 2010, 12:11
par Nightmare » 23 Fév 2010, 12:11
Comment en être si persuadé? As-tu vu une démonstration du calcul de cette limite qui commençait ainsi?
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 23 Fév 2010, 12:19
par benekire2 » 23 Fév 2010, 12:19
Ben passé un temps en fouillant sur le net il y a de ça quelques temps, je crois avoir vu une preuve élémentaire, que j'avais compris, donc ça suppose au maximum que la preuve était de niveau début de sup.
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 23 Fév 2010, 12:27
par benekire2 » 23 Fév 2010, 12:27
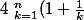^k \le e^n \le \Bigprod_{k=1}^{n}(1+\frac{1}{k})^{k+1})
On réécrit (si je ne me suis pas trompé) :
^n}{n!} \le e^n \le \frac{(n+1)^{n+1}}{n!})
Ça y est c'est mieux comme ça, il me semble que l'on peut se servir de ça ... mais comment ? Je cherche encore...
PS: J'ai fais le con, j'ai modifié tout le message d'avant ... merde !

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 23 Fév 2010, 13:04
par Ben314 » 23 Fév 2010, 13:04
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 23 Fév 2010, 13:22
par benekire2 » 23 Fév 2010, 13:22
Oui effectivement la preuve est bien :we:
Je viens à l'instant de me rendre compte que quand j'avais fait u(n+1)/u(n) et bien j'avais pas remplacé tout les n par n+1 ... sick
Néanmoins (têtu comme trois mules) je vais essayer de conclure ma preuve avec l'encadrement .. même si j'ai pas l'impression que ça va débouché sur quelque chose!
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 23 Fév 2010, 13:29
par benekire2 » 23 Fév 2010, 13:29
Je fais appel à vous ...
Je sais maintenant que :
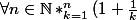^k \le e^n \le \Bigprod_{k=1}^{n}(1+\frac{1}{k})^{k+1})
Je voudrais savoir quel est la forme la plus simplifiée de ces deux produits ?
Est-ce que c'est :
^n}{n!} \le e^n \le \frac{(n+1)^{n+1}}{n!})
Ou peut-on faire mieux ?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 23 Fév 2010, 13:42
par Ben314 » 23 Fév 2010, 13:42
Ta preuve fonctionne parfaitement bien:
On montre que
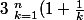^k \le e^n \le \Bigprod_{k=1}^{n}(1+\frac{1}{k})^{k+1})
en partant du fait que
\leq x)
sur

(que l'on démontre faisant les tableaux de variations des différences)
On en déduit effectivement que
^n}{n!} \le e^n \le \frac{(n+1)^{n+1}}{n!})
qui signifie que
^n \le n! \le (n+1)\left(\frac{n+1}{e}\right)^n)
et que
^{\frac{1}{n}} \le (n+1)^{\frac{1}{n}}\ \frac{1+\frac{1}{n}}{e})
Il ne reste plus qu'a montrer que
^{\frac{1}{n}})
tend vers 1 à l'aide du logarithme et de l'exponentielle...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités