Continuité et périodicité
18 messages
- Page 1 sur 1
continuité et périodicité
Bonjour j'ai besoin de votre aide pr en exercice. Le voilà :
soit f une fonction pèriodique de période 2 telle que pr tout x appartenant à [0,2[ f(x)=sin(pi*x)+ax+1
montrer que f est continue en R ssi a=0.
Merci d'avancee.
soit f une fonction pèriodique de période 2 telle que pr tout x appartenant à [0,2[ f(x)=sin(pi*x)+ax+1
montrer que f est continue en R ssi a=0.
Merci d'avancee.
Re: continuité et périodicité
lalaliii23877 a écrit:Bonjour j'ai besoin de votre aide pr en exercice. Le voilà :
soit f une fonction pèriodique de période 2 telle que pr tout x appartenant à [0,2[ f(x)=sin(pi*x)+ax+1
montrer que f est continue en R ssi a=0.
Merci d'avancee.
Re: continuité et périodicité
lalaliii23877 a écrit:Bonjour j'ai besoin de votre aide pr en exercice. Le voilà :
soit f une fonction pèriodique de période 2 telle que pr tout x appartenant à [0,2[ f(x)=sin(pi*x)+ax+1
montrer que f est continue en R ssi a=0.
Merci d'avancee.
Salut,
As-tu essayé de regarder à quoi ressemble le graphe de f ?
Par exemple pour a = 1, ou a = 2 ou a = -1 ?
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: continuité et périodicité
Bonjour,
Quelle est la définition de "continuité" ?
En quelles valeurs de l'intervalle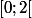 la fonction est-elle continue ?
la fonction est-elle continue ?
Par suite, en quelles valeurs de l'intervalle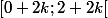 la fonction est-elle continue ?
la fonction est-elle continue ?
Il faut alors en déduire les points particuliers pour lesquels une attention doit être portée.
Quelle est la définition de "continuité" ?
En quelles valeurs de l'intervalle
Par suite, en quelles valeurs de l'intervalle
Il faut alors en déduire les points particuliers pour lesquels une attention doit être portée.
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: continuité et périodicité
Lostounet a écrit:lalaliii23877 a écrit:Bonjour j'ai besoin de votre aide pr en exercice. Le voilà :
soit f une fonction pèriodique de période 2 telle que pr tout x appartenant à [0,2[ f(x)=sin(pi*x)+ax+1
montrer que f est continue en R ssi a=0.
Merci d'avancee.
Salut,
As-tu essayé de regarder à quoi ressemble le graphe de f ?
Par exemple pour a = 1, ou a = 2 ou a = -1 ?
non je n 'ai pas tracé le graphe. Mais est ce que ça m aidera dèmontrer ?
Re: continuité et périodicité
Pourquoi je te proposerais de tracer la fonction si ça n'aidait pas à se faire une idée de ce qu'il faut démontrer?
Après, à toi de voir si tu as envie de le faire ou non.
Après, à toi de voir si tu as envie de le faire ou non.
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: continuité et périodicité
Lostounet a écrit:Pourquoi je te proposerais de tracer la fonction si ça n'aidait pas à se faire une idée de ce qu'il faut démontrer?
Après, à toi de voir si tu as envie de le faire ou non.
Bien sûr que j ai envie de le faire. si vs voulez bien m'expliquer les étapes que je devrai procéder afin de démontrer ça m'aiderait.
Re: continuité et périodicité
Ce que veut dire Lostounet, c'est que faire un dessin ça aide à "voir ce qui se passe", donc à trouver exactement ce qui est à démontrer.
Si tu as Geogebra, par exemple, trace la fonction avec : tu verras tout de suite où sont les points de discontinuité. Cela te permettras de répondre à ma question "est-ce que la fonction est continue sur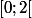 puis sur
puis sur 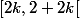 etc.
etc.
Le "dessin" en math n'est jamais une démonstration, mais c'est un excelent moyen de comprendre ce qui se passe.
Si tu as Geogebra, par exemple, trace la fonction avec : tu verras tout de suite où sont les points de discontinuité. Cela te permettras de répondre à ma question "est-ce que la fonction est continue sur
Le "dessin" en math n'est jamais une démonstration, mais c'est un excelent moyen de comprendre ce qui se passe.
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: continuité et périodicité
Perso, j'aurais commencé par chercher "a" pour que f soit périodique de période 2.
Re: continuité et périodicité
Lostounet a écrit:Salut,
As-tu essayé de regarder à quoi ressemble le graphe de f ?
Par exemple pour a = 1, ou a = 2 ou a = -1 ?
c'est de loin la meilleure indication
chercher une non périodicité en supposant que la période est 2 ne mène à aucun résultat général.
en traçant la fonction, tu aurais surtout remarqué que a≠0 => la limite de la fonction en +oo est ±oo
ceci ne prouve rien encore (cf arctan(x))
Mais, soit M un nombre positif sur [0;M], f est bornées sur [0;M] => f n'atteint pas ±oo =>...
est-ce que sa période peut être ≤ M ?
Re: continuité et périodicité
Bonjour
Je pense que c'est un très bon réflexe que de revenir aux graphes de façon presque systématique.
Parce que=\sin(\pi x)+a x+ 1) (pour a différent de zéro) on doit voir que ça ressemble à peu près
(pour a différent de zéro) on doit voir que ça ressemble à peu près
à "quelque chose qui oscille autour d'une droite oblique".
Ce qui rejoins alors la remarque de Nogdim que la fonction n'est pas périodique.
D'où la bizarrerie de l'exercice. En effet, il laisse croire à première lecture que la fonction et 2- périodique
pour tout a et seulement continue pour a=0.
A mon avis je pense qu'il faut corriger un peu l'énoncé.
Montrer que la fonction périodique ssi a=0 et
continue pour tout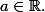
Lostounet a écrit:As-tu essayé de regarder à quoi ressemble le graphe de f ?
Par exemple pour a = 1, ou a = 2 ou a = -1 ?
Je pense que c'est un très bon réflexe que de revenir aux graphes de façon presque systématique.
Parce que
à "quelque chose qui oscille autour d'une droite oblique".
Ce qui rejoins alors la remarque de Nogdim que la fonction n'est pas périodique.
D'où la bizarrerie de l'exercice. En effet, il laisse croire à première lecture que la fonction et 2- périodique
pour tout a et seulement continue pour a=0.
A mon avis je pense qu'il faut corriger un peu l'énoncé.
Montrer que la fonction périodique ssi a=0 et
continue pour tout
Re: continuité et périodicité
Repartons du départ sans se laisser influencer par les réponses déjà données :
soit f une fonction périodique de période 2 telle que pr tout x appartenant à [0,2[ f(x)=sin(pi*x)+ax+1
montrer que f est continue en R ssi a=0.
par définition f continue sur [0,2[
il faut ensuite regarder si, a minima, f continue en 0 et 2, or f est aussi 2-périodique.
il faut que : f(2-) = f(0) pour que la fonction soit continue en 2
et on a une équation qui revient à : a=0
On s'est compliqué la vie
soit f une fonction périodique de période 2 telle que pr tout x appartenant à [0,2[ f(x)=sin(pi*x)+ax+1
montrer que f est continue en R ssi a=0.
par définition f continue sur [0,2[
il faut ensuite regarder si, a minima, f continue en 0 et 2, or f est aussi 2-périodique.
il faut que : f(2-) = f(0) pour que la fonction soit continue en 2
et on a une équation qui revient à : a=0
On s'est compliqué la vie
Re: continuité et périodicité
pascal16 a écrit:par définition f continue sur [0,2[
Je suis désolé mais même si tu repars à zéro la fonction est continue sur
La seule chose à relever c'est que pour l'énoncé ça ne vas pas.
Et là c'est toi qui complique. Je ne sais pas si le posteur va s'y retrouver.
Re: continuité et périodicité
soit f une fonction pèriodique de période 2 telle que pr tout x appartenant à [0,2[ f(x)=sin(pi*x)+ax+1
la fonction f est définie sur [0,2[ par f(x)=sin(pi*x)+ax+1, elle est donc continue sur [0;2[
en dehors de [0;2[, f est définie par par sa périodicité de période 2 et non pas par la relation f(x)=sin(pi*x)+ax+1.
l'énoncé est bon
la question est en fait : " pour que le raccord par périodicité se fasse, quelle(s) valeur(s) peut prendre a"
la fonction f est définie sur [0,2[ par f(x)=sin(pi*x)+ax+1, elle est donc continue sur [0;2[
en dehors de [0;2[, f est définie par par sa périodicité de période 2 et non pas par la relation f(x)=sin(pi*x)+ax+1.
l'énoncé est bon
la question est en fait : " pour que le raccord par périodicité se fasse, quelle(s) valeur(s) peut prendre a"
Re: continuité et périodicité

n'est-ce pas comme cela qu'il faut comprendre l'énoncé?
On définit une fonction sur [0; 2[ et on la prolonge sur R par 2-périodicité.
Et ensuite on cherche le "a" pour avoir le raccord par continuité ?
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: continuité et périodicité
commentaire de l'image : votre ressort de suspension avant et après un Paris-Dakar.
18 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 33 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
