Bonsoir,
Attention: ce n'est pas parce que les trois cotés sont tangents au cercle inscrit que tu tombes forcément sur le bon triangle: tu peux tracer une infinité de triangles différents avec ce même cercle inscrit. Mais peu d'entre eux auront un périmètre et une surface donnée...
pascal16 a écrit:deux triangles de surface identiques ne sont pas forcément des triangles identiques.
est-ce que tu as une figure qui te donne une particularité sur le triangle (isocèle, rectangle... ) ?
Il est clair que connaître seulement le périmètre d'un triangle n'est pas suffisant pour retrouver les trois cotés: c'est facile à voir.
Aussi, comme le dit Pascal, deux triangles de surface identique ne sont pas forcément identiques, donc n'ont pas forcément les cotés égaux...
Après, on peut se demander (ce qui semble être le but de l'exercice), si connaître à la fois l'aire et le périmètre en même temps permet de trouver a, b et c (les trois longueurs). D'ailleurs, il semblerait qu'ils aient tous le même rayon pour le cercle inscrit (vu la formule que tu cites)!
Et la réponse est... non.
Par exemple, on peut déjà rappeler la formule de Héron qui stipule que
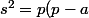(p - b)(p - c))
avec p le demi-périmètre de triangle.. Or cette formule indique par exemple que les triangles de cotés 25,34,39 et 29,29,40 (par exemple) ont même périmètre mais aussi même aire... et ces triangles sont bien différents (et même, on peut avoir un troisième candidat 24,37,37).
Donc ce qu'on pourrait chercher à faire (peut-être pas la manière la plus élégante, ni celle demandée par l'énoncé directement), c'est essayer d'exprimer deux cotés du triangle (par exemple a et b) en fonction de p et c. Pour chaque c que tu choisis (donc tu traces une tangente au cercle et tu fixes la longueur du segment c que tu choisis), tu auras la possibilité d'exprimer a et b en fonction de ce c, et donc de tracer un bon candidat.
Sauf erreur de ma part, cela se fait assez bien à l'aide de la formule de Héron à l'aide d'un petit changement d'inconnues.
 . Qu'est ce qui ne va pas??
. Qu'est ce qui ne va pas??
