Conjecture et preuve

[lillyyyyy]

Bonjour, je doit faire un dm de math mais je suis un peu bloqué vers la fin.

L'énoncé étant le suivant:
1. Tracer dans un repère orthonormé la courbe representative de la fonction f définie sur l'ensemble des réels par: f(x)=x², et le cercle de centre A(0;1) et de rayon 1.
On se demande si la courbe représentative de f et le cercle se supperposent sur un petit intervalle proche de la valeur 0.
Pouvez vous conjecturer une réponse à cette question ?

J'ai tout simplement répondu que je pensais que le cercle et la courbe ne se supperposent que en 0 (car même 0.01²=0.0001

Le problème étant pour moi dans la question seconde:
2. prendre un point M appartenant à la courbe représentative de la fonction f.
Résolvez l'quation AM²=1
Conclure

J'ai commencé en choisissant M=(2;4), mais je ne sais vraiment pas comment continuer mon idée...

[mamanprof]

Pour la question 1, as-tu fait le dessin ?
Si tu l'as fait, tu as dû constater que ta parabole et ton cercle se coupent en 2 points : l'origine (0;0) et un autre point.

Je ne vois pas en quoi le fait que 0,01² = 0,0001 justifie ta réponse...

Pour la deuxième question, on te demande de prendre un point au hasard sur la parabole.
Un tel point a pour coordonnées .

Rappel :

Remplace et 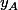par les bonnes valeurs.

[lillyyyyy]

AM²= (x;0)²+(f(x)-1)² ?

[mamanprof]

AM²= (x-0)²+(f(x)-1)² ?

Oui.
Remplace f(x) par x² maintenant.

[lillyyyyy]

AM²= (x-0)²+(x²-1)² ?

AM²= x²+ (x²-1)² ??

[mamanprof]

AM²= (x-0)²+(x²-1)² ?

AM²= x²+ (x²-1)² ??

Oui.
Maintenant résouds l'équation :

[lillyyyyy]

(x²-1)²=x²
x^4-1=x²
-1=x²-x^4
-1=x-² ?

[mamanprof]

(x²-1)²=x²
x^4-1=x²
-1=x²-x^4
-1=x-² ?

C'est faux dès la première ligne...
Développe plutôt (x²-1)² dans l'équation à résoudre.

[lillyyyyy]

oulalah je vais déprimer..

x²+(x²-1)²=1
x²+x²-1Xx²-1=1 ?

[lillyyyyy]

ou
x²+(x²-1)²=1
x²+x^4 - 2x² + 1=1 ?

[lillyyyyy]

et donc x²+(x²-1)²=1
x²+x4 - 2x² + 1=1
x^6-2x²+1=1
x^6-2 X x²+1=1
x^6-x^4+1=1
x²+1=1 ?? :)

[mathafou]

Bonjour,
voir aussi la discussion identique de lillyyyyy sur l'ile des maths