Preuve/application du binôme de Newton
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Cptain Guguss
- Membre Naturel
- Messages: 18
- Enregistré le: 02 Juin 2013, 18:52
-
 par Cptain Guguss » 04 Juin 2013, 18:09
par Cptain Guguss » 04 Juin 2013, 18:09
chan79 a écrit:Salut
On peut démontrer d'abord que
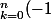^{k} k C_{n}^{k}=0)
en effet
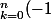^{k} k C_{n}^{k}=\bigsum_{k=1}^{n}(-1)^{k} k C_{n}^{k}=\bigsum_{k=1}^{n}(-1)^{k}k\fra{n!}{k!(n-k)!})
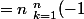^{k}\fra{(n-1)!}{(k-1)!(n-k)!}=n\ \bigsum_{k=0}^{n-1}(-1)^{k+1}C_{n-1}^{k}=-n(1-1)^{n-1}=0)
on fait de même avec
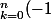^{k} k(k-1) C_{n}^{k}=0)
on en déduit
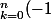^{k} k^{2} C_{n}^{k}=0)
puis
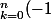^{k} k^{3} C_{n}^{k}=0)
jusqu'à
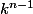
un peu long à rédiger mais ça devrait marcher, j'espère ...
Merci beaucoup je regarde ça ce soir

-
Robic
- Membre Irrationnel
- Messages: 1084
- Enregistré le: 03 Mai 2013, 11:00
-
 par Robic » 05 Juin 2013, 04:59
par Robic » 05 Juin 2013, 04:59
C'est quand même particulièrement difficile pour le niveau de 1ère S ! (même en fait pour la terminale)

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 05 Juin 2013, 05:39
par chan79 » 05 Juin 2013, 05:39
Robic a écrit:C'est quand même particulièrement difficile pour le niveau de 1ère S ! (même en fait pour la terminale)
IL y a peut-être plus simple; je ne vois pas ... :triste:
-
Robic
- Membre Irrationnel
- Messages: 1084
- Enregistré le: 03 Mai 2013, 11:00
-
 par Robic » 05 Juin 2013, 07:00
par Robic » 05 Juin 2013, 07:00
Je me suis mal exprimé : ce n'était pas une critique de ta réponse, mais de la question de départ. Justement, je ne vois pas plus simple non plus, du coup je me dis : qu'est-ce qu'ils leur prend de donner à des élèves de première des exercices pareils...
(Peut-être que Cptain Guguss est dans une école de surdoué... ?)
-
Cptain Guguss
- Membre Naturel
- Messages: 18
- Enregistré le: 02 Juin 2013, 18:52
-
 par Cptain Guguss » 05 Juin 2013, 20:13
par Cptain Guguss » 05 Juin 2013, 20:13
Robic a écrit:Je me suis mal exprimé : ce n'était pas une critique de ta réponse, mais de la question de départ. Justement, je ne vois pas plus simple non plus, du coup je me dis : qu'est-ce qu'ils leur prend de donner à des élèves de première des exercices pareils...
(Peut-être que Cptain Guguss est dans une école de surdoué... ?)
Non, je ne suis pas dans une ecole de surdoué

... et cet exercice n'est pas obligatoire à faire, mais le prof nous a dit que c'était faisable pour un première, mais que nous allions en baver... et c'est le cas.
-
Cptain Guguss
- Membre Naturel
- Messages: 18
- Enregistré le: 02 Juin 2013, 18:52
-
 par Cptain Guguss » 05 Juin 2013, 20:37
par Cptain Guguss » 05 Juin 2013, 20:37
Chan79, quand tu dis :
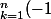^{k}k\fra{n!}{k!(n-k)!}=n\ \bigsum_{k=1}^{n}(-1)^{k}\fra{(n-1)!}{(k-1)!(n-k)!}=n\ \bigsum_{k=1}^{n}(-1)^{k}\fra{(n-1)!}{(k-1)!(n-k)!}=n\ \bigsum_{k=0}^{n-1}(-1)^{k+1}C_{n-1}^{k})
Il y a une petite chose que je ne comprend pas. Comment obtient-on

avec
!}{(k-1)!(n-k)!})
... ne devrait-on pas avoir
!}{k!(n-1-k)!})
?
-
Cptain Guguss
- Membre Naturel
- Messages: 18
- Enregistré le: 02 Juin 2013, 18:52
-
 par Cptain Guguss » 05 Juin 2013, 20:38
par Cptain Guguss » 05 Juin 2013, 20:38
Cptain Guguss a écrit:Chan79, quand tu dis :
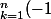^{k}k\fra{n!}{k!(n-k)!}=n\ \bigsum_{k=1}^{n}(-1)^{k}\fra{(n-1)!}{(k-1)!(n-k)!}=n\ \bigsum_{k=1}^{n}(-1)^{k}\fra{(n-1)!}{(k-1)!(n-k)!}=n\ \bigsum_{k=0}^{n-1}(-1)^{k+1}C_{n-1}^{k})
Il y a une petite chose que je ne comprend pas. Comment obtient-on

avec
!}{(k-1)!(n-k)!})
... ne devrait-on pas avoir
!}{k!(n-1-k)!})
?
Le changement de la valeur initiale de k ?

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 05 Juin 2013, 20:52
par chan79 » 05 Juin 2013, 20:52
Cptain Guguss a écrit:Chan79, quand tu dis :
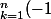^{k}k\fra{n!}{k!(n-k)!}=n\ \bigsum_{k=1}^{n}(-1)^{k}\fra{(n-1)!}{(k-1)!(n-k)!}=n\ \bigsum_{k=1}^{n}(-1)^{k}\fra{(n-1)!}{(k-1)!(n-k)!}=n\ \bigsum_{k=0}^{n-1}(-1)^{k+1}C_{n-1}^{k})
Il y a une petite chose que je ne comprend pas. Comment obtient-on

avec
!}{(k-1)!(n-k)!})
... ne devrait-on pas avoir
!}{k!(n-1-k)!})
?
Exact ! Bien remarqué !
J'aurais dû détailler:
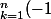^{k}k\fra{n!}{k!(n-k)!}=n\ \bigsum_{k=1}^{n}(-1)^{k}\fra{(n-1)!}{(k-1)!(n-k)!}=n\ \bigsum_{k=1}^{n}(-1)^{k}\fra{(n-1)!}{(k-1)!(n-k)!})
Je pose k'=k-1
quand k varie de 1 à n, alors k' varie de 0 à n-1
On remplace k par k'+1
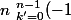^{k'+1}\fra{(n-1)!}{k'!(n-k'-1)!})
si on remet k à la place de k'
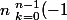^{k+1}\fra{(n-1)!}{k!(n-k-1)!})
^{k+1}=-(-1)^k)
je passe le moins devant
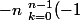^k \fra{(n-1)!}{k!(n-k-1)!})
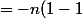^{n-1}=0)
-
Cptain Guguss
- Membre Naturel
- Messages: 18
- Enregistré le: 02 Juin 2013, 18:52
-
 par Cptain Guguss » 05 Juin 2013, 21:10
par Cptain Guguss » 05 Juin 2013, 21:10
chan79 a écrit:Exact ! Bien remarqué !
J'aurais dû détailler:
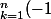^{k}k\fra{n!}{k!(n-k)!}=n\ \bigsum_{k=1}^{n}(-1)^{k}\fra{(n-1)!}{(k-1)!(n-k)!}=n\ \bigsum_{k=1}^{n}(-1)^{k}\fra{(n-1)!}{(k-1)!(n-k)!})
Je pose k'=k-1
quand k varie de 1 à n, alors k' varie de 0 à n-1
On remplace k par k'+1
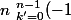^{k'+1}\fra{(n-1)!}{k'!(n-k'-1)!})
si on remet k à la place de k'
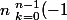^{k+1}\fra{(n-1)!}{k!(n-k-1)!})
^{k+1}=-(-1)^k)
je passe le moins devant
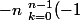^k \fra{(n-1)!}{k!(n-k-1)!})
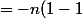^{n-1}=0)
Merci

Pour le calcul avec k(k-1), je pose k'=k-2, c'est bien ca ?

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 05 Juin 2013, 21:17
par chan79 » 05 Juin 2013, 21:17
Cptain Guguss a écrit:Merci

Pour le calcul avec k(k-1), je pose k'=k-2, c'est bien ca ?
c'est ça. Bon courage :zen:
-
Cptain Guguss
- Membre Naturel
- Messages: 18
- Enregistré le: 02 Juin 2013, 18:52
-
 par Cptain Guguss » 05 Juin 2013, 21:19
par Cptain Guguss » 05 Juin 2013, 21:19
chan79 a écrit:c'est ça. Bon courage :zen:
Et j'ai (encore) une question... Comment "deduit-on" le resultat pour k² ?

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 06 Juin 2013, 05:45
par chan79 » 06 Juin 2013, 05:45
Cptain Guguss a écrit:Et j'ai (encore) une question... Comment "deduit-on" le resultat pour k² ?
on sait que:
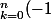^{k} k C_{n}^{k}=0)
et
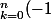^{k} k(k-1) C_{n}^{k}=0)
on ajoute et ça donne:
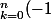^{k} (k+k^2 -k)C_{n}^{k}=0)
soit
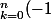^{k} k^2 C_{n}^{k}=0)
Un conseil
pour bien comprendre la suite, faire tous les calculs avec n=5 par exemple
-
Cptain Guguss
- Membre Naturel
- Messages: 18
- Enregistré le: 02 Juin 2013, 18:52
-
 par Cptain Guguss » 06 Juin 2013, 20:02
par Cptain Guguss » 06 Juin 2013, 20:02
chan79 a écrit:on sait que:
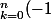^{k} k C_{n}^{k}=0)
et
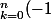^{k} k(k-1) C_{n}^{k}=0)
on ajoute et ça donne:
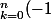^{k} (k+k^2 -k)C_{n}^{k}=0)
soit
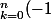^{k} k^2 C_{n}^{k}=0)
Un conseil
pour bien comprendre la suite, faire tous les calculs avec n=5 par exemple
Je ne comprends pas comment on "ajoute" les deux égalités... On fait un système ?
-
Cptain Guguss
- Membre Naturel
- Messages: 18
- Enregistré le: 02 Juin 2013, 18:52
-
 par Cptain Guguss » 06 Juin 2013, 21:50
par Cptain Guguss » 06 Juin 2013, 21:50
Je viens de finir de rédiger la preuve "au propre" et je la rends demain.
Merci beaucoup chan79 pour ton aide :happy3:
Et merci aussi à Robic, Kikoo <3 bieber, LeJeu et Archibald de s'être penchés sur mon problème :lol3:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités
avec
... ne devrait-on pas avoir
?