Congruence

par **sue** » 26 Déc 2006, 23:46

salut,

je bloque sur cette question :

déterminer les restes de la division euclidienne par 4 des nombres

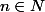
un indice ?

merci :we:

par **crassus** » 27 Déc 2006, 00:22

dejà des que n est superieur ou egal à 2 cette somme a meme reste que 3^n +1 ( car 2^n+4^n est divisible par 4 des que n>ou= 2) or 3^n est congru à(-1)^n modulo 4 car 3 congru à -1 modulo 4 ... finalement cette somme pour n superieur ou egal a deux se trouve congru à 1+(-1)^n modulo 4 ... suivant la parité de n , on trouve que cette somme est congru à 0 ou 2 modulo 4 ... donc si n pair superieur ou egal a 2 le reste est 2 si n impair superieur à 2 , le reste est nul , enfin si n=0 le reste est nul et si n=1 le reste vaut 2 ... ce qui constitue deux cas particuliers à considerer ...

par **babaz** » 27 Déc 2006, 11:48

Plus simplement, je ferais un tableau de congruences modulo 4, qui synthétiserait tout ce que vous avez exposé.

par **sue** » 27 Déc 2006, 13:13

ok , merci à vous :we:

par **sue** » 27 Déc 2006, 14:20

re,

voilà mnt j'ai

je veux montrer que :

dois-je utiliser un résonnement par reccurence ?

par **BancH** » 27 Déc 2006, 15:03

Nan, sans récurrence.

Il suffit de dire que le reste de

dans la division euclidienne par

a pour période

:

Donc

et

par **sue** » 27 Déc 2006, 15:18

ok ok , merci Banch :we:

Congruence

congruence

Qui est en ligne