Congruence

[pirox]

Bonsoir,

J'ai 2 démonstration à faire mais je vois vraiment pas comment faire.

Définition: soit a et b deux entiers on dit que a et b sont congru modulo n si b-a et un multiple de n on note "a et congru a b mod n " sous la forme "a≡b mod(n)"

<=>(1) a≡b mod(n)
<=>(2)[a]n = n
<=>(3) a et b ont le même reste dans la division euclidienne par n

Démontrer que (1) <=> (2) par construction/définition des classe de congruence mod n
(1) <=> (3): on doit démontré que (1) => (3) (1) <= (3)

[b]voici mon début de réponse

montrons que a et b congru entre eux modulo n est équivalent au reste de la division euclidienne de a et b par n.
Démontrons les 2 implication.
supposons 2 entier a et b tel que a≡b mod(n)

b-a = nk je doit prouver quoi ? dire que a et b congru entre eux modulo n sa veux dire [a]n = [b]n ? donc je doit dire quoi ? que [a]n = [b]n et que la reste de la division euclidienne de a et b ces a=qn+r et b=q'n+r' et donc r=r' mais alors comment démontrer que r=r'?

[GaBuZoMeu]

S'il te plaît, corrige ton message en faisant la différence entre "et" et "est", entre a et à.
Aussi, évite d'écrire b entre crochets sans espace, parce que html croit que c'est une balise "boldface". Écris plutôt [ b ], avec des espaces.
On se comprendra déjà beaucoup mieux.

[pirox]

Bonjour,

Je ne suis pas expert en orthographe mais dit moi si autre chose n'est pas clair !

Définition: soit a et b deux entiers on dit que a et b sont congru modulo n si b-a est un multiple de n on note "a et congru à b mod n " sous la forme "a≡b mod(n)"

<=>(1) a≡b mod(n)
<=>(2)[a]n = [ b ]n
<=>(3) a et b ont le même reste dans la division euclidienne par n

Démontrer que (1) <=> (2) par construction/définition des classe de congruence mod n
(1) <=> (3): on doit démontré que (1) => (3) (1) <= (3)

voici mon début de réponse

montrons que a et b congru entre eux modulo n est équivalent au reste de la division euclidienne de a et b par n.
Démontrons les 2 implication.
supposons 2 entier a et b tel que a≡b mod(n)

b-a = nk je doit prouver quoi ? dire que a et b congru entre eux modulo n sa veux dire [a]n = [ b ]n ? donc je doit dire quoi ? que [a]n = [ b ]n et que la reste de la division euclidienne de a et b ces a=qn+r et b=q'n+r' et donc r=r' mais alors comment démontrer que r=r'?

[GaBuZoMeu]

Il reste encore un "et" à la place de "est". Ce n'est pas tant une question d'orthographe qu'une question de compréhension du sens logique de la phrase, ce qui est embêtant quand on fait des maths.

Pour démontrer l'équivalence de 1 et 2, on doit bien sûr utiliser la définition de que tu n'as pas donnée. Je devine bien sûr de quoi il s'agit, mais la rédaction de la démonstration dépend de la forme de la définition qui t'a été donnée.

Pour l'équivalence de 1 et 3, il s'agit de démontrer que a-b est divisible par n si et seulement si a et b ont même reste dans la division par n. Montre l"implication dans un sens, puis l'implication dans l'autre sens.

[pirox]

Okay la si tu me dit que il y a encore un et de travers je vois pas ou il est

Définition: soit a et b deux entiers on dit que a et b sont congru modulo n si b-a est un multiple de n on note "a est(j'avais pas vu celui ci) congru à b mod n " sous la forme "a≡b mod(n)"

<=>(1) a≡b mod(n)
<=>(2)[a]n = [ b ]n
<=>(3) a et b ont le même reste dans la division euclidienne par n

Démontrer que (1) <=> (2) par construction/définition des classe de congruence mod n
(1) <=> (3): on doit démontré que (1) => (3) (1) <= (3)

voici mon début de réponse

montrons que a et b congru entre eux modulo n est équivalent au reste de la division euclidienne de a et b par n.
Démontrons les 2 implication.
supposons 2 entier a et b tel que a≡b mod(n)

b-a = nk je doit prouver quoi ? dire que a et b congru entre eux modulo n sa veux dire [a]n = [ b ]n ? donc je doit dire quoi ? que [a]n = [ b ]n et que la reste de la division euclidienne de a et b ces a=qn+r et b=q'n+r' et donc r=r' mais alors comment démontrer que r=r'?

Définition de [ a ]n
on définit classe de a modulo n comme étant l'ensemble de tous les entier congru à a modulo n.
je n'ai pas comprit il suffit d’énoncer la définition pour démontrer l'équivalence de 1 et 2 ? si oui bah là voilà démontré !

donc je doit démontrer que a et b ont le même reste dans la division euclidienne donc dans ma tête il ce passe ça
a=qn+r ---> n=qr+r' ---> r=qr'+r'' etc.. et b=q'n+r''''''--->n=q'+r''''''''..... alors les reste sont forcément égaux à 0 car si on continue à l'infinie on tombera sur le PGCD puis 0 mais du coup je ne vois pas la différence entre le PGCD et la division euclidienne

maintenant démontrons que a-b et divisible par n si tel est le cas alors il existe un entier k tel que a-b=nk

enfaite j'arrive pas du tous à savoir ce que je doit déduire de ça que r=r' ? que a = b ? où un autre chose ?

[GaBuZoMeu]

Quel mélange !!!

Comme je l'ai écrit, la définition de va influer sur la rédaction de la démonstration. Je n'ai jamais écrit qu'il suffisait d'écrire la définition pour avoir une démonstration.

Supposons la propriété 2
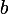est congru à lui-même, donc . D'après la définition de , on a .
On a montré que 2 implique 1.

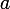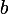Supposons la propriété 1. Ceci veut dire que divise , donc il existe un entier tel que . Effectuons la division euclidienne de par : avec . Alors , donc est aussi le reste de la division euclidienne de par .
On a montré que 1 implique 3.

Je te laisse démontrer les autres implications. En fait, pour montrer l'équivalence des trois propriétés, il suffirait de montrer en plus que 3 implique 2.

[pirox]

b est congru à lui-même comment le sait tu ? [ b ]n veux dire b congru à b ?

Supposons la propriété 3.
{a]n={ b ]n si nous reprenons la définition qui dit que [ a ]n représente tous les entier modulo alors {a]n={ b ]n = a≡b mod(n) et soit a et b deux entiers on dit que a et b sont congru modulo n si b-a est un multiple de n alors il existe un entier k tel que b-a=nk Effectuons la division euclidienne de a par n : a =nq+r avec 0⩽r<n . Alors b=a+b-a=n(q+k)+r , donc r est aussi le reste de la division euclidienne de b par n .

j'ai l'impression d'avoir démontré 2 implique 3 et pas 3 implique 2 mais si je ne dit pas d'abord le pourquoi du comment j'ai pu démontré que les reste de a et b sont identique alors je ne peu pas dire que 3 implique 2 à

ici je ne sait pas que b-a est un multiple de n car je doit d'abord démontré 3 donc je fait un calcul qui ma l'air plutôt faux moins de dire que j'ai démontré que avant que 1 implique 3 alors je sait que les reste de la division euclidienne de a et b sont identique donc plus que à dire :

Effectuons la division euclidienne de a par n : a =nq+r avec 0⩽r<n . Alors b=a+b-a=n(q+k)+r , donc r est aussi le reste de la division euclidienne de b par n et comme a≡b mod(n) si est seulement si a-b est multiple de n alors a-b = nk donc j'ai démontré l'implication de 1 dans 3 enfaite. serte j'ai définit 3 en premier pour à la fin dire que j'ai réussie à faire ce calcul grâce à 1.

je sait je suis pas très malin !

[GaBuZoMeu]

b est congru à lui-même comment le sait tu ?

En appliquant la définition : n divise b-b.

[ b ]n veux dire b congru à b ?

Cette question n'a pas de sens. Que veux-tu dire ?

Désolé, mais j'ai le plus grand mal à comprendre ce que tu écris. Essaie de faire des phrases claires. Une démonstration, c'est un texte en français qui doit être bien écrit, facilement compréhensible.

Pour montrer que 3 implique 2 :
On suppose que et ont même reste dans la division euclidienne par , et il faut en déduire que . Il faut donc montrer que tout entier congru à modulo est congru à modulo , et réciproquement.