Congruence.....petit exo a deux méth..!!!demonde d'éxplicati
41 messages
- Page 1 sur 3 - 1, 2, 3
congruence.....petit exo a deux méth..!!!demonde d'éxplicati
bonjour voilà l'énnoncé : démontrer que pour tout entier naturel n )
voiçi ma méthode :
on destingue 6 cas .
si alors
alors^7 +6(7k) = 0(9)) et puis de meme je le montre pour les cas suivants :
et puis de meme je le montre pour les cas suivants :






mais dans un livre j'ai trouvé une autre méthode que j' ai pas compris . là voilà : toutes les congruences qui suivent sont modulo 7
 donc pour tout entier n ,
donc pour tout entier n , 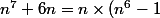) on en déduit que pour tout entier n ,
on en déduit que pour tout entier n , 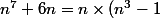 ( n^3+1)) le problème est donc de démontrer que pour tout entier n ,
le problème est donc de démontrer que pour tout entier n , (n^3+1) = 0) (congrus à 0)
(congrus à 0)
si n congru 0 alors)
si n n'est pas congru à 0 modulo 7 étudions pour les autres valeurs quels sont les restes modulo 7 de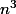 aprés ils ont fait un tableau
aprés ils ont fait un tableau
n 1 2 3 4 5 6
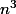 1 1 6 1 6 6
1 1 6 1 6 6
si on remarque que 6 congru -1 , on voit que ds tous les cas (sauf 0 étudié avant ) ,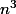 est congru soit à 1 soit à -1 et donc
est congru soit à 1 soit à -1 et donc (n^3+1)) congru 0 ce qui achève la démonstration
congru 0 ce qui achève la démonstration
ouffffffff
on destingue 6 cas .
si
mais dans un livre j'ai trouvé une autre méthode que j' ai pas compris . là voilà : toutes les congruences qui suivent sont modulo 7
si n congru 0 alors
si n n'est pas congru à 0 modulo 7 étudions pour les autres valeurs quels sont les restes modulo 7 de
n 1 2 3 4 5 6
si on remarque que 6 congru -1 , on voit que ds tous les cas (sauf 0 étudié avant ) ,
ouffffffff
citation : posté par flodlarab
Je préfères la mienne ... elle ne fait pas appel à un éclair de génie mais une bonne vieille méthode classique .
:ptdr:
il n'ya pas d'éclair de génie ds ma mthode quand meme
quand tu veux montrer qu)
il suffit de montrer que est divisible par sept c'est pour ça que j'ai destingué les 7 cas là .......!!!!!!!!!!!!!!!!!!!!! :marteau:
est divisible par sept c'est pour ça que j'ai destingué les 7 cas là .......!!!!!!!!!!!!!!!!!!!!! :marteau:
Je préfères la mienne ... elle ne fait pas appel à un éclair de génie mais une bonne vieille méthode classique .
:ptdr:
il n'ya pas d'éclair de génie ds ma mthode quand meme
quand tu veux montrer qu
il suffit de montrer que
citation :
nnnnnnnnnnnnnnn
c'est pas qu' on sait pas développer en terminale s , mais c'est que l'objectif des congruence c'est pas de savoir développer mais d'utiliser les proprietés de divisibilité ............ect
en plus en maths c'est pas trés intelligent de penser à développer un truc assez grand
ily'a des methodes trés simples
c nouveau ? On sait pas développer en terminale S ?
nnnnnnnnnnnnnnn
c'est pas qu' on sait pas développer en terminale s , mais c'est que l'objectif des congruence c'est pas de savoir développer mais d'utiliser les proprietés de divisibilité ............ect
en plus en maths c'est pas trés intelligent de penser à développer un truc assez grand
ily'a des methodes trés simples
41 messages
- Page 1 sur 3 - 1, 2, 3
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 57 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
