Congruence.....petit exo a deux méth..!!!demonde d'éxplicati
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 31 Oct 2006, 12:44
par Flodelarab » 31 Oct 2006, 12:44
(Ce qu'il y a de bien avec l'informatique, c que le copier/coller coute pas cher)récurrence:
- Au rang 0: 0=0 [7]
- Au rang n, je le suppose vrai
- Au rang n+1, prouvons le
^7 + 6(n+1) = n^7 + 7n^6 + 21n^5 + 35n^4 + 35n^3 + 21n^2 + 7n + 1 + 6n +6 = n^7 + 6n +7(n^6 + 3n^5 + 5n^4 + 5n^3 + 3n^2 + n + 1) = 0 (mod 7))
CQFD
ok?
-
izamane95
- Membre Rationnel
- Messages: 620
- Enregistré le: 31 Aoû 2006, 22:08
-
 par izamane95 » 31 Oct 2006, 12:58
par izamane95 » 31 Oct 2006, 12:58
ok :king2:
:hein: mais un truc me surprend : pour quoi tu compend pas la méthode que j'ai trouvé dans mon livre :hein: :hein: :hein: :hein:
quand tu veux montrer par exemple que le nombre n = ab (a²-b²)= 0(3) ne me dit pas que la aussi tu panse à utiliser la récurrence :ptdr:
ms en utilisant un peut d'eclair de génie :ptdr: tu remarque que le reste ds la division par 3 d'un entier est 0,1,2 donc a et b st congru à 0;1 ou 2 (3)
aprés tu fais :
x 0 1 2
x² 0 1 1
et là le résultat est immédiat
ça revient quand meme à la méthode de mon livre là ..............
nn????? ou ça sent léclair de génie?
-
prody-G
- Membre Relatif
- Messages: 376
- Enregistré le: 28 Mar 2006, 14:36
-
 par prody-G » 31 Oct 2006, 13:00
par prody-G » 31 Oct 2006, 13:00
moi jpense ça serait plus simple de factoriser par n déjà non?
comme ça : n^7+6n cong 0 mod(7)
<--> n cong 0 mod(7) ou n^6+6n cong 0 mod(7)
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 31 Oct 2006, 13:05
par Quidam » 31 Oct 2006, 13:05
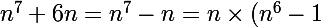\ \ \ [7])
Mais puisque 7 est premier, on sait que

, donc :
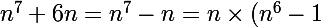=0\ \ \ [7])
Voilà !
-
izamane95
- Membre Rationnel
- Messages: 620
- Enregistré le: 31 Aoû 2006, 22:08
-
 par izamane95 » 31 Oct 2006, 13:06
par izamane95 » 31 Oct 2006, 13:06
allez- y prody - g
montrez moi votre méthode ça m'aidera
-
prody-G
- Membre Relatif
- Messages: 376
- Enregistré le: 28 Mar 2006, 14:36
-
 par prody-G » 31 Oct 2006, 13:09
par prody-G » 31 Oct 2006, 13:09
lol ouai ça marche aussi...
on peut pas faire plus court jpense
par contre comment tu sais que n^6 est congru à 1 mod(7) ?
-
izamane95
- Membre Rationnel
- Messages: 620
- Enregistré le: 31 Aoû 2006, 22:08
-
 par izamane95 » 31 Oct 2006, 13:13
par izamane95 » 31 Oct 2006, 13:13
mais pourquoi

d'ailleurs :doh:
-
prody-G
- Membre Relatif
- Messages: 376
- Enregistré le: 28 Mar 2006, 14:36
-
 par prody-G » 31 Oct 2006, 13:18
par prody-G » 31 Oct 2006, 13:18
bah parce que c'est modulo 7
tu "déroule" 7n et 6n cong -n mod (7)
-
prody-G
- Membre Relatif
- Messages: 376
- Enregistré le: 28 Mar 2006, 14:36
-
 par prody-G » 31 Oct 2006, 13:27
par prody-G » 31 Oct 2006, 13:27
si n = 7k alors n^6 cong 0 mod (7) et pas à 1 non?
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 31 Oct 2006, 13:28
par Quidam » 31 Oct 2006, 13:28
prody-G a écrit:lol ouai ça marche aussi...
on peut pas faire plus court jpense
par contre comment tu sais que n^6 est congru à 1 mod(7) ?
Ben c'est un théorème du cours non ?
Si p est premier,

! J'y peux rien ! C'est la loi !
Sauf erreur...
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 31 Oct 2006, 13:30
par Quidam » 31 Oct 2006, 13:30
izamane95 a écrit:mais pourquoi

d'ailleurs :doh:
Parce que

-
izamane95
- Membre Rationnel
- Messages: 620
- Enregistré le: 31 Aoû 2006, 22:08
-
 par izamane95 » 31 Oct 2006, 13:31
par izamane95 » 31 Oct 2006, 13:31
ah ok
autre question : pour montrer par exemple que pour tout n,
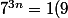)
il suffit de dire qu'on a 7= -2(9) donc
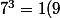)
donc
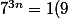)
ou il faut le démontrer par récurrence?????????????
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 31 Oct 2006, 13:33
par Quidam » 31 Oct 2006, 13:33
prody-G a écrit:si n = 7k alors n^6 cong 0 mod (7) et pas à 1 non?
C'est juste, c'est l'exception, que j'avais oublié de mentionner ! Mais dans ce cas

aussi non ?
-
izamane95
- Membre Rationnel
- Messages: 620
- Enregistré le: 31 Aoû 2006, 22:08
-
 par izamane95 » 31 Oct 2006, 13:39
par izamane95 » 31 Oct 2006, 13:39
j'attend toujours une réponce pour mon exemple
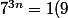)
:euh:
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 31 Oct 2006, 13:41
par Quidam » 31 Oct 2006, 13:41
izamane95 a écrit:ah ok
autre question : pour montrer par exemple que pour tout n,
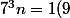)
il suffit de dire qu'on a 7= -2(9) donc
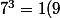)
donc
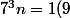)
ou il faut le démontrer par récurrence?????????????
Eh, attends ! Tu veux dire
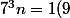)
ou
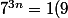)
?
Parce que
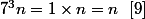
qui n'est pas toujours égal à 1 !
J'en déduis que tu veux montrer que

Ben pour ça tu écris effectivement :

OK ?
Il n'y a pas de récurrence, sauf triviale : pas la peine de le mentionner !
-
prody-G
- Membre Relatif
- Messages: 376
- Enregistré le: 28 Mar 2006, 14:36
-
 par prody-G » 31 Oct 2006, 13:42
par prody-G » 31 Oct 2006, 13:42
bah faut que tu prennes en compte n et pas seulement 7^3.
-
izamane95
- Membre Rationnel
- Messages: 620
- Enregistré le: 31 Aoû 2006, 22:08
-
 par izamane95 » 31 Oct 2006, 13:42
par izamane95 » 31 Oct 2006, 13:42
exusez moi regarder la derniere modification
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 31 Oct 2006, 13:46
par Quidam » 31 Oct 2006, 13:46
izamane95 a écrit:j'attend toujours une réponce pour mon exemple
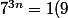)
:euh:
Ouais, dix minutes pour répondre ! C'est inadmissible, n'est-ce pas ?
Si tu veux avoir des réponses, faudrait voir à ne pas nous prendre pour des esclaves !
-
izamane95
- Membre Rationnel
- Messages: 620
- Enregistré le: 31 Aoû 2006, 22:08
-
 par izamane95 » 31 Oct 2006, 13:48
par izamane95 » 31 Oct 2006, 13:48
du calme ..........du calme , j'aime pas le mot esclave d'ailleur :triste:
j'ai juste dit que je l'attend .......c'est tout
-
izamane95
- Membre Rationnel
- Messages: 620
- Enregistré le: 31 Aoû 2006, 22:08
-
 par izamane95 » 31 Oct 2006, 13:51
par izamane95 » 31 Oct 2006, 13:51
grand merci pour vos eclircissement en tout cas :++:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 65 invités
il suffit de dire qu'on a 7= -2(9) donc
donc
ou il faut le démontrer par récurrence?????????????