Concour général

[and1dx]

Bonjour je voudrais savoir si ma démonstration est juste:


Démontrer que

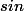
Comme est croissante sur [0;pi/2] et x est positif donc





Donc on peut en déduire l'égalite initial c'est bon ou pas ?

[and1dx]

up .

[Ericovitchi]

ha non car tu dois démontrer ton inégalité pour tout x entre 0 et pi/2 et là tu te sers d'une limite au voisinage de zéro.

Tu as démontré que ton inégalité finissait par être vraie pour un x assez proche de zéro mais pas qu'elle est vraie pour tout x entre 0 et pi/2.

Essayes autre chose comme de montrer que le sinus qui est convexe vers le bas, est au dessus de sa corde entre 0 et pi/2 (c'est ce que veut dire ton inégalité en fait).
Ou bien autre méthode tu étudies la fonction sinx - (2/Pi)x en la dérivant, et en montrant qu'elle est positive.

[and1dx]

Ok merci .