Concavité d'une droite

[jankyjack]

Bonsoir,

j'aimerai savoir si une droite est convexe, concave ou bien les deux.

parce que je sais qu'une fonction est convexe si sa dérivée seconde est supérieur ou égal à 0. donc quand je dérive deux fois l'équation d'une droite c'est égal à 0. donc c 'est pourquoi je me pose la question

[capitaine nuggets]

Salut !

La terminologie est inexacte : si tu te places dans un cadre fonctionnel (si tu travailles avec des fonctions), on parle de convexité (resp. concavité) pour des fonctions et non pas pour leur courbe représentative.

Dans le plan muni d'un repère orthonormé, soient la fonction définie par , où et sont deux réels quelconques, et la courbe représentative de ( représente n'importe quelle droite du plan à l'exception d'une : celle d'équation qu'il faudrait traiter à part). est dérivable une infinité de fois car c'est une fonction polynomiale et . Or si et seulement si et et :
- équivaut à dire que est concave ;
- équivaut à dire que est convexe (c'est la raison que tu as cité).
Donc est à la fois convexe et concave.

Néanmoins, si tu as un doute, tu peux revenir à la définition : soit une fonction définie sur et la courbe représentative de . On dit que est convexe (resp. concave) si pour tous réels 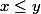, on a (resp. ).

[pascal16]

résumé : Une droite est concave et convexe, les inégalités sont au sens large.
Tout comme le nombre 0 est positif et négatif (au sens large).

[Pseuda]

Bonjour,

En d'autres termes, si on dérive 2 fois une fonction affine f telle que f(x)=ax+b, dont la courbe représentative est une droite (non parallèle à (Oy) l'axe des ordonnées), tu as remarqué que f''=0.

Ceci veut dire qu'une fonction dont la courbe représentative est une droite, est par définition, à la fois convexe (f''>=0) et concave (f''<=0).

[jankyjack]

okay merci des réponses