Complexes
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
omidkohsan
- Membre Naturel
- Messages: 31
- Enregistré le: 17 Mar 2007, 22:22
-
 par omidkohsan » 09 Juin 2007, 12:24
par omidkohsan » 09 Juin 2007, 12:24
On donne l'équation
z^4-2R²cos2wz²+R^4=0
w et R appartiennent au Réels
a)calculer les racines et représenter ces racines dans le plan de Gauss
b) Si g1,g2,g3,g4 sont des racines
alors z1^n+z2^n+z3^n+z4^n=0 si n est impair
=4R^n10(nw) si n est pair
aidez moi silvouplai :mur: :stupid_in
-
biotop
- Membre Naturel
- Messages: 20
- Enregistré le: 09 Juin 2007, 09:18
-
 par biotop » 09 Juin 2007, 12:45
par biotop » 09 Juin 2007, 12:45
euh je suis incapable de faire mais jai juste une question, tu es en terminale ? je suis sensée savoir faire ça pour le bac ??? je sais même pas ce que cets le plan de gauss ><'
-
annick
- Habitué(e)
- Messages: 6291
- Enregistré le: 16 Sep 2006, 09:52
-
 par annick » 09 Juin 2007, 13:56
par annick » 09 Juin 2007, 13:56
bonjour,
je te donne déjà le démarrage :
tu poses Z=z² donc
Z²-2R²cos(2w)Z+R^4=0
delta=4R^4cos²(2w)-4R^4=4R^4(cos²(2w)-1)=-4R^4sin²(2w)=4R^4sin²(2w)i=
(2R²sin(2w))²
Tu peux donc trouver tes solutions en Z
Bon courage pour avancer
-
Yawgmoth
- Membre Relatif
- Messages: 206
- Enregistré le: 06 Jan 2007, 23:17
-
 par Yawgmoth » 09 Juin 2007, 14:00
par Yawgmoth » 09 Juin 2007, 14:00
Hello,
EDIT : Annick, veux-tu que j'efface mon message ?
Tu poses
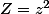
 Z + R^4=0)
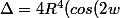)^2 - 4. R^4)
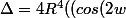)^2 - 1))
 +- \sqrt {\Delta}}{2})
Ensuite, vu que tu as posé que
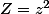
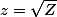
N'oublie pas que comme tu travailles dans les complexes, avoir l'intérieur d'une racine qui est négatif ne pose pas problème

.
-
omidkohsan
- Membre Naturel
- Messages: 31
- Enregistré le: 17 Mar 2007, 22:22
-
 par omidkohsan » 09 Juin 2007, 22:39
par omidkohsan » 09 Juin 2007, 22:39
merci annick
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 84 invités
