Comparaison de deux nombres irrationnels

[CrazyShoot]

Bonjour,

Actuellement en pré DAEU B, avec le CNED je lutte avec la comparaison des racines carrées.
J'ai utilisé l'identité remarquable pour la première, mais je n'arrive pas pour la deuxième. Je trouve un résultat différent du leurs.

Je n'arrive pas à trouver un cours plus explicite.





Merci,.

[Black Jack]

Bonjour,
Le b de l'énoncé est

c'est différent du b que tu as utilisé qui est

Et donc, forcément, tes résultats sont faux.

[CrazyShoot]

Bonjour,

Je n'ai pas tout saisi, comment calculer

?

Merci,

[Black Jack]

Bonjour,

Je n'ai pas tout saisi, comment calculer

?

Merci,

Drôle de question ...

C'est immédiat, du moins si on sait ce qu'est une racine carrée et une élévation au carré.



C'est absolument à comprendre avant de poursuivre quoi que soit dans ce genre de calculs.

[catamat]

Bonjour

La définition dont parle Blackjack dit que :

la racine carrée de est un réel positif dont le carré est égal à

[CrazyShoot]

Bonjour,

Oui, j'ai compris 5²=25 donc = 5.
J'ai bon ? Oui...

Mais alors A=B ? Car ils sont pareil ?

[CrazyShoot]

Si A²=B² Alors A=B ou A=-B.
A=-B ? Je n'ai pas compris ?

J'ai compris cela.
x² - 36 = 0
x² - 6² = 0
(x-6) ou (x+6)
Donc x=6 ou x=-6.

[CrazyShoot]

Voici l'aide du cned que j'ai reçu.

https://ibb.co/ZGcq5S4
https://ibb.co/4VQR3K1

[lyceen95]

Retourne à l'exercice.
Ligne à ligne. Quelle est la ligne où tu décroches.
On nous donne a = une certaine formule, et b = une autre formule.

Ils calculent a²
Ils calculent b²
Ils constatent que a² et b², c'est exactement la même chose.
Ils disent que a est négatif
Ils disent que b est positif
Ils concluent en disant que a=-b

Si tu es d'accord avec chacune des étapes du calcul, si tu sais reproduire chaque étape du calcul, sans regarder le corrigé, ça roule.
Mais apparemment, il y a des étapes qui te gènent.

[CrazyShoot]

Toutes les lignes...

[catamat]

Je pense que tu n'écrirais pas que 6 est égal à -6 pourtant on a 6²=(-6)²
En fait 6 est l'opposé de -6

Ici c'est la même chose on a a²=b² mais on ne peut pas écrire que a et b sont égaux car ils sont de signes contraires donc ils sont opposés. (il n'y a pas d'autres possibilités ils sont soit égaux soit opposés)

[CrazyShoot]

Je me suis complètement perdu.

[annick]

Bonjour,

tu as écrit : "Si A²=B² Alors A=B ou A=-B.
A=-B ? Je n'ai pas compris ?"

En fait en repartant dans l'autre sens, on voit que ça marche :

A=B, si on élève au carré, donne bien A²=B²

A=-B, si on élève au carré donne (A)²=(-B)², soit A²=B² car on a aussi élevé le signe - au carré, ce qui donne +.

Donc, quand on se trouvera en face d'une expression qui dit A²=B², il ne faudra jamais oublier qu'il y aura 2 solutions : soit A=B, soit A=-B.

[annick]

Bonjour,

Je n'ai pas tout saisi, comment calculer

?

Merci,

Drôle de question ...

C'est immédiat, du moins si on sait ce qu'est une racine carrée et une élévation au carré.



C'est absolument à comprendre avant de poursuivre quoi que soit dans ce genre de calculs.

Crazyshoot s'est bien présenté comme ayant quitté sa scolarité très jeune et sa démarche est de tout reprendre à zéro pour passer un Pré DAEU .
Il est donc assez normal qu'il ait des questions qui te paraissent évidentes mais qui sont loin de l'être pour lui.
Alors, encourageons sa démarche qui est courageuse plutôt que de lui signifier que ses lacunes sont un puits sans fond

[CrazyShoot]

Bonsoir, annick merci,

Je commence un peu à comprendre, un peu.

Donc j’élève au carré les deux nombres irrationnels.

Le carré annule la racine, mais alors ? Pourquoi pas

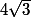
Je vais me faire tuer.

J'utilise l'identité remarquable pour calculer A, et comme j'ai élevé au carré B alors racine de 4 devient 4.
Alors, j'obtiens les deux même valeurs.

Après comme a² = b² = 0, alors c'est soit a = b ou a = -b, car comme tu as dit.

mais après ?


Oui, j'ai quitté ma scolarité trop jeune. Hélas je ne peux revenir en arrière, mais je peux changer mon futur. Je l’espère.

Je travaille sur les maths depuis la mi novembre, toutes les journées, et tout les jours.
Malheureusement pour moi les lacunes sont là, et les espoirs et la motivation baisse.
Je ne veux pas baisser les bras, j'ai abandonné tellement de fois.
Ma vie est tellement vide, je veux juste avoir un DAEU...
...

[annick]

Pourquoi reviens-tu à (2V3)² ?
Ton nombre b est V(4-2V3). Donc b²=4-2V3 (il suffit juste d'enlever la grande racine qui englobe tout)

Excuse-moi de ne pas écrire en latex, je ne le maitrise toujours pas bien !!! A la place du signe "racine carrée, je mets donc un V.

Et pour répondre à la fin e ton précédent message, je suis certaine qu'en travaillant régulièrement, tu peux l'avoir ce DAEU. Je connais plusieurs personnes qui ont ainsi pu le réussir et repartir sur de bonnes bases, alors pourquoi pas toi ? Ne lâches rien et tu pourras y arriver.

[CrazyShoot]

Bonjour,

J'ai un peu mieux compris aujourd'hui.

Cependant je lutte encore avec la fin.
Soit c'est A = B ou A = - B.

B=

A= positif si et négatif si

donc 1 < < 2 Alors A est négatif.

mais c'est A=-B, mais c'est A qui est négatif ? alors c'est -a=b ?

ou alors -b c'est A ? c'est ça ?

Merci

[catamat]

Quand on écrit a=-b le signe moins signifie "opposé de", donc : "a est égal à l'opposé de b".

Cela n'indique pas le signe de ces nombres, si ce n'est que l'un est positif et l'autre négatif

Par ex : 5 est l'opposé de -5 s'écrit 5=-(-5)

[CrazyShoot]

Donc oui, -B, c'est A.

Je pense avoir compris, je vais mettre de côté et passer à une autre leçon.
Il me faudrait des cours en présentiel.

[CrazyShoot]

J'ai oublié merci,