Comparaison de deux nombres irrationnels

[mathelot]

bonjour,
autre méthode,autre exercice

[CrazyShoot]

Bonjour,
Merci, mathelot c'est encore plus compliqué pour moi.

Je voulais juste savoir pourquoi, c'est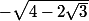 alors qu'il est positif. Pourquoi le moins est devant ?

https://ibb.co/gmXtzYG

Merci,

[annick]

Si tu es d'accord sur le fait que A=B ou A=-B, on peut repartir de là.

A=1-V3, V3 est sensiblement égal à 1,732, donc 1-V3 est négatif.
B=V(4-2V3), or une racine est toujours positive, donc B ne peut être que positif.

Un nombre négatif ne peut pas être égal à un nombre positif, donc A ne peut pas être égal à B.

Donc A est forcément égal à -B, soit 1-V3=- V(4-2V3).

Tu peux essayer de vérifier tout ça sur ta calculatrice.

[CrazyShoot]

Bonsoir,

Oui, j'ai compris que les deux résultats sont égaux sauf que c'est soit A=B ou alors A=-B.

A=1-V3, oui il est négatif car 1-1.73 = -0.73, donc négatif.

B=V(4-2V3), une racine est toujours positive, OUI.

Un nombre négatif ne peut être égal à un nombre positif Je n'ai pas très bien compris.
Tu veux dire qu'un nombre négatif est différent d'un positif, je pense que c'est cela.

Mais, pourquoi c'est - V(4-2V3), alors qu'il est positif ?
Il est négatif alors qu'il est positif, ou alors c'est pour dire qu'il est différent de A ?

J'en suis vraiment navré.

[CrazyShoot]

J'apprécie vraiment vos aides à tous, merci. Bonne soirée.

[Jérôme]

Dans ton exemple, quand tu as une racine carrée qui prend un nombre en entier, mettre au carré enlève cette racine carrée car la racine carrée est intuitivement le "contraire" de mettre au carré.

a=1-racine(3) est négatif car racine(3) est supérieur à 1.
En mettant a au carré, on voit que c'est égal à b au carré.
Or deux carrés sont égaux si les nombres sont égaux ou opposés.
Par exzmple 5 et-5 sont opposés et si tu les mets au carré ils sont égaux à 25.
Donc comme a est négatif et b est positif, ils ne sont pas égaux, et comme leurs carrés sont égaux, la seule solution restante est que a et b sont opposés : a=-b .

[CrazyShoot]

Oui, j'ai compris cela, je me demandais juste pourquoi, c'est -(4-2V3) alors qu'il est positif, pourquoi il y a un moins devant alors qu'il est positif.
J'ai un peu de mal à expliquer cela.

[Jérôme]

a=-b, le moins vient de là.

[CrazyShoot]

a=-b, le moins vient de là.

Bonjour,

C'est clair là.

Merci, pour cette précision.