Merci !!

vam a écrit:à part le fait de montrer que AH est inférieur à AC et aussi à AI (en prenant les notations de la figure)
sauf si quelqu'un a une autre idée...
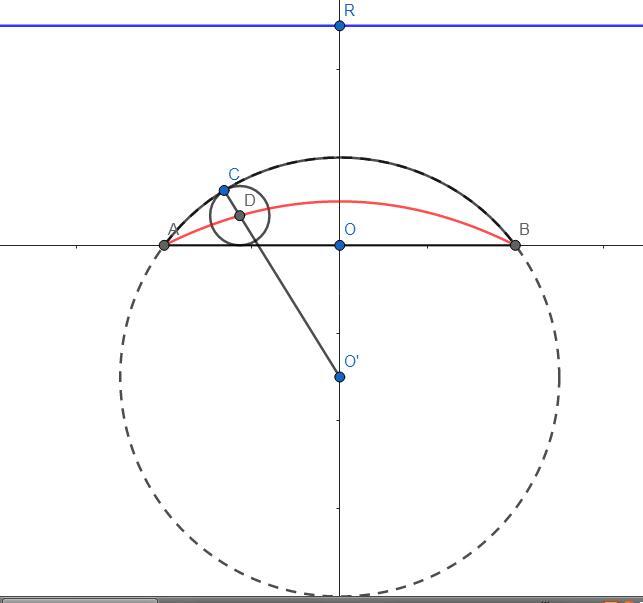
GaBuZoMeu a écrit:Plus la corde est grande, et plus la flèche est grande, et la flèche est le diamètre du plus grand cercle contenu dans l'espace entre la corde et l'arc.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 57 invités
Tu pars déja ?
Identification
Pas encore inscrit ?
Ou identifiez-vous :